[ad_1]
Right here we are going to be taught multiplying 2-digit quantity by 1-digit
quantity. In two other ways we are going to be taught to multiply a two-digit quantity by a
one-digit quantity.
Examples of multiplying 2-digit quantity by 1-digit quantity with out Regrouping:
We could have a fast overview of multiplication of 2-digit quantity by 1-digit quantity with out regrouping:
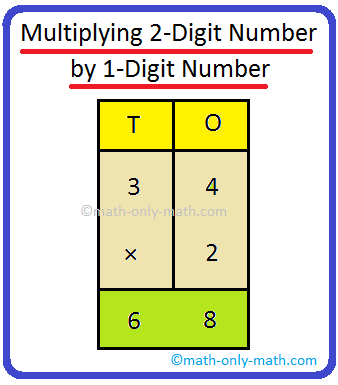
1. Multiply 24 by 2.
|
T O 2 4 × 2 4 8 |
First multiply those by 2. 4 × 2 = 8. Write 8 underneath O. Now multiply the tens by 2. 3 × 3 = 9. Write 9 underneath T. |
2. Multiply 34 and a pair of
Resolution:
|
Step I: Prepare the numbers vertically. Step II: First multiply the digit on the ones place by 2. 2 × 4 = 8 ones Step III: Now multiply the digit on the tens place by 2. 2 × 3 = 6 tens |
Thus, 34 × 2 = 68 |
3. Multiply 20 by 3 by utilizing expanded kind
Resolution:
20 → 2 tens + 0 ones
× 3 → × 3
6 tens + 0 ones
= 60 + 0
= 60
Due to this fact, 20 × 3 = 60
4. Multiply 50 by 1 by utilizing quick kind
Resolution:
50 → 50
× 1 → × 1
0 50
(i) First digit of 1’s place is multiplied by 1, i.e., 0 × 1 = 0
(ii) Then digit at ten’s place is multiplied by 1, i.e., 5 tens × 1 = 5 tens
Therefore, 50 × 1 = 50
Observe the next Instance utilizing Three Completely different Strategies:
5. Multiply 13 by 2.
Resolution:
First Methodology: Utilizing Repeated Addition.
13 x 2 = 13 + 13 = 26
Due to this fact, 13 x 2 = 26.
Second Methodology: Utilizing Expanded Kind
Contemplate 13 as 10 + 3.
13 × 2 = (10 + 3) × 2
= 10 × 2 + 3 × 2
= 20 + 6
= 26.
Third Methodology: Quick Kind
Write the numbers in response to place worth proven on the suitable.
Step I:
Multiply those:
3 ones × 2 = 6 ones
Write 6 underneath ones column.
Step II:
Multiply the tens:
1 ten × 2 = 2 tens
Write 2 underneath tens column.
Thus, the product of 13 and a pair of is 26.
Examples of multiplying 2-digit quantity by 1-digit quantity with Regrouping:
1. Multiply 66 by 3
|
T O 1 6 6 × 3 1 4 8 |
First multiply those by 3. 6 × 3 = 18 = one ten + 8 ones Write 8 underneath O. carry 1 ten Now multiply the tens by 3. 6 × 3 = 18 Add 1 to the product. 18 + 1 = 19 |
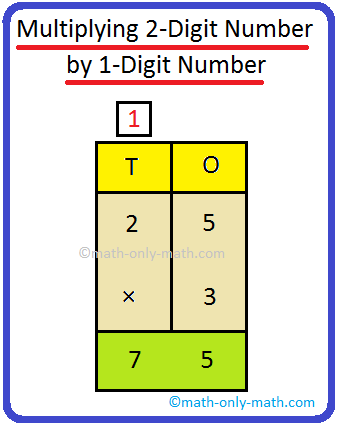
2. Multiply 25 by 3
|
Step I: Prepare the numbers vertically. Step II: First multiply the digit on the ones place by 3. 3 × 5 = 15 = 1 ten + 5 ones Write 5 within the ones column and carry over 1 to the tens Step III: Now multiply the digit on the tens place by 3. 3 × 2 = 6 tens Now, 6 + 1 (carry over) = 7 tens |
Thus, 25 × 3 = 75 |
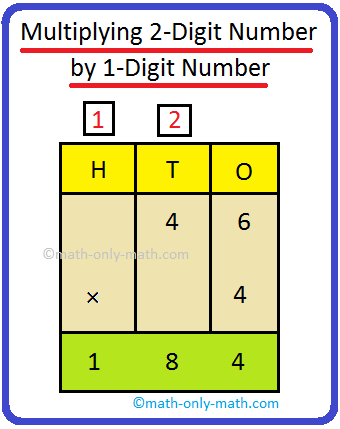
3. Multiply 46 by 4
|
Step I: Prepare the numbers vertically. Step II: Multiply the digit on the ones place by 4. 6 × 4 = 24 = 2 tens + 4 ones Write 4 within the ones column and carry over 2 to the tens Step III: Now multiply the digit on the tens place by 4. 4 × 4 = 16 tens Now, 16 + 2 (carry over) = 18 tens = 1 hundred + 8 tens Write 8 on the tens place and 1 on the hundred place. |
Thus, |
4. Multiply 20 by 3 by utilizing expanded kind
Resolution:
20 → 2 tens + 0 ones
× 3 → × 3
6 tens + 0 ones
= 60 + 0
= 60
Due to this fact, 20 × 3 = 60
5. Multiply 26 by
7 by utilizing expanded kind
Resolution:
26 → 20 + 6 → 2 tens + 6 ones
× 7 → × 7 → × 7
(2 × 7) tens + (6 ×
7) ones
2 tens + 6 ones
× 7 ones
14 tens + 42 ones
= 14 tens + (40 + 2) ones
= 14 tens + 4 tens + 2 ones
= 18 tens + 2 ones
= 180 + 2
= 182
Due to this fact, 26 × 7 = 182
6. Multiply 48 by
6 by utilizing quick kind
Resolution:
48
× 6
24 ← 48
= 28 tens 8 ones
= 288
Therefore, 48 × 6 = 288
(i) 48 × 6 is written in column from.
(ii) 8 ones are multiplied by 6, i.e., 6 × 8 = 48 ones = 4
tens + 8 ones
8 is written is one’s column and 4 tens is gained.
(iii) Gained 4 is carried to the ten’s column.
(iv) Now 4 tens is multiplied by 6, i.e., 4 tens × 6 = 24
tens
(v) Carried 4 tens is added to 24 tens, i.e., 4 tens + 24
tens = 28 tens
7. Discover the
product of 58 × 5.
Resolution:
58
× 5
25 ← 40
= 25 + 4 ← 0
= 29 0
= 290
(i) 8 ones × 5 = 40 = 4 tens + 0 one
(ii) 5 tens × 5 = 25 tens
(iii) 25 tens + 4 tens = 29 tens
Therefore, 58 × 5 = 290
8. Multiply 37 by
8
Resolution:
3 7
× 8
5 6
+ 2 4 0
2 9 6
(i) 7 ones × 8 = 56 ones = 5 tens 6 ones
56 is positioned in such method that 5 comes underneath tens and 6 underneath
ones
(ii) 3 tens × 8 = 24 tens = 240 ones
= 2 a whole lot, 4 tens and 0 ones
240 is positioned under 56 in such method that 2 comes underneath a whole lot,
4 underneath tens and 0 underneath ones.
Therefore, 37 × 8 = 296
Questions and Solutions on Multiplying 2-Digit Quantity by 1-Digit Quantity:
Multiplication of 2-Digit Quantity by 1-Digit Quantity With out Regrouping:
I. Discover the product:
(i) 23 × 3 =
(ii) 44 × 2 =
(iii) 33 × 2 =
(iv) 22 × 4 =
(v) 32 × 3 =
(vi) 40 × 2 =
(vii) 43 × 2 =
(viii) 12 × 3 =
(ix) 23 × 2 =
(x) 11 × 9 =
(xi) 21 × 4 =
(xii) 13 × 3 =
Reply:
I. (i) 69
(ii) 88
(iii) 66
(iv) 44
(v) 96
(vi) 80
(vii) 86
(viii) 36
(ix) 46
(x) 99
(xi) 84
(xii) 39
Multiplication of 2-Digit Quantity by 1-Digit Quantity With Regrouping:
II. Discover the product:
(i) 46 × 2
(ii) 19 × 4
(iii) 27 × 3
(iv) 18 × 5
Reply:
II. (i) 92
(ii) 76
(iii) 81
(iv) 90
III. Multiply the next:
(i) 78 × 4
(ii) 63 × 6
(iii) 51 × 6
(iv) 39 × 8
(v) 72 × 9
(vi) 45 × 7
(vii) 17 × 4
(viii) 88 × 8
Reply:
III. (i) 312
(ii) 398
(iii) 306
(iv) 312
(v) 648
(vi) 315
(vii) 68
(viii) 704
IV. Remedy the next:
(i) 37 × 6
(ii) 72 × 4
(iii) 56 × 7
(iv) 84 × 2
(v) 45 × 9
Reply:
IV. (i) 37 × 6
(ii) 72 × 4
(iii) 56 × 7
(iv) 84 × 2
(v) 45 × 9
V. Multiply the next :
|
(i) T O 3 1 × 2 _______ |
(ii) T O 4 7 × 1 _______ |
|
(iii) T O 1 1 × 3 _______ |
(iv) T O 2 2 × 2 _______ |
|
(v) T O 2 3 × 2 _______ |
(vi) T O 2 6 × 3 _______ |
|
(vii) T O 4 9 × 2 _______ |
(viii) T O 2 3 × 4 _______ |
|
(ix) T O 1 6 × 6 _______ |
(x) T O 1 9 × 5 _______ |
|
(xi) T O 5 2 × 5 _______ |
(xii) T O 2 3 × 6 _______ |
|
(xiii) T O 6 4 × 9 _______ |
(xiv) T O 3 2 × 7 _______ |
|
(xv) T O 7 5 × 8 _______ |
VI. Multiply the next:
(i) 21 × 5 = _____
(ii) 34 × 2 = _____
(iii) 23 × 3 = _____
(iv) 27 × 3 = _____
(v) 38 × 2 = _____
(vi) 18 × 4 = _____
(vii) 25 × 8 = _____
(viii) 32 × 6 = _____
(ix) 29 × 4 = _____
(x) 45 × 5 = _____
From Multiplying 2-Digit Quantity by 1-Digit Quantity to HOME PAGE
Did not discover what you had been in search of? Or wish to know extra info
about Math Solely Math.
Use this Google Search to seek out what you want.
[ad_2]