The place worth of a digit in a quantity is the worth it holds to be
on the place within the quantity. We all know in regards to the place worth and face worth
of a digit and we are going to find out about it in particulars.

We all know
that every digit in a quantity has a spot. The place {that a} digit occupies in a quantity
tells us about its place worth.

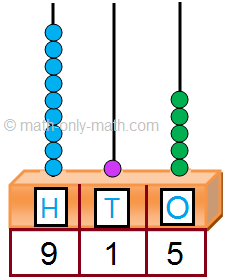
Allow us to
take a 3-digit quantity 915

So, the
place worth of digit 9 is 9 hundred or 900.

The place
worth of digit 1 is 1 ten or 10.

The place
worth of digit 5 is 5 ones or 5.

Place, Place Worth and Face Worth: 

A quantity is fashioned by grouping the digits collectively. 

● Every digit has a hard and fast place referred to as its place. 

● Every digit has a price relying on its place referred to as the place worth of the digit. 

● The face worth of a digit for anywhere within the given quantity is the worth of the digit itself 

● Place worth of a digit = (face worth of the digit) × (worth of the place) 

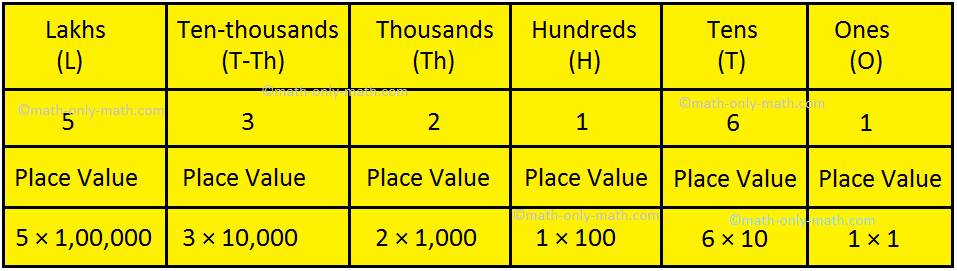
We all know
that every digit in a quantity has a spot worth. The place a digit occupies in a
quantity tells us its place worth. So, the product of the digit and the worth of
the place it occupies provides us the place worth. Allow us to prepare the digits of
the quantity 5, 32,161 within the following place worth chart.

The face
worth of a digit in a quantity is the digit itself.

Properties of Place Worth:

1. The place worth of each one-digit quantity is identical as and equal to its face worth. 

(i) Place worth and face worth of 1, 2, 3, 4, 5, 6, 7, 8 and 9 are 1, 2, 3, 4, 5, 6, 7, 8 and 9 respectively.

(ii) The place worth of zero (0) is at all times 0. It could maintain anywhere in a quantity, its worth is at all times 0.

As, in 105, 350, 42017, 90218 the place worth of 0 in every quantity is 0.

2. In a two-digit quantity, the place worth of the ten-place digit is 10 instances of the digit.

As, in 58, the place worth of 5 is 5 × 10 = 50 and place worth of 8 is 8 × 1= 8; the face worth of 5 is 5 and of 8 is 8.

3. Within the quantity 475, the digit 5 is at one’s place, digit 7 is at ten’s place and digit 4 is at hundred’s place.

So, place worth of 5 = 5, place worth of seven = 7 × 10 = 70, and place worth of 4 is 4 × 100 = 400.

Thus, for the place worth of a digit, the digit is multiplied by the place worth of 1 it needs to be that place.

For Instance:

In 768;

the place worth of 8 = 8 × 1 = 8

the place worth of 6 = 6 × 10 = 60 and

the place worth of seven is 7 × 100 = 700.

4. Now it’s the basic legislation that the digit possesses its place
worth because the product of the digit and place worth of 1 to be at that
place. 

For Instance:

(i) In a quantity 4129; 

the place worth of 9 is 9 × 1 = 9 as 9 is at one’s or unit’s place.

the place worth of two is 2 × 10 = 20 as 2 is at ten’s place.

the place worth of 1 is 1 × 100 = 100 as 1 is at hundred’s place.

the place worth of 4 is 4 × 1000 = 4000 as 4 is at thousand’s place.

(ii) In a quantity 3720, the place worth of

(iii) Place worth of the digits 3702 are proven under:

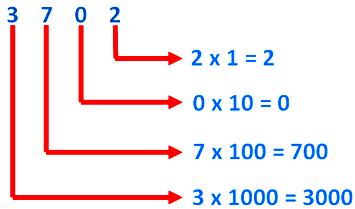
(iv) Right here, we additionally see that the place worth of the digit 0 in a quantity is at all times zero, no matter could also be its place.

Place-value of a Digit in a Quantity:

We all know that the place of a digit in a quantity determines
its corresponding worth within the quantity. Allow us to take into account the quantity 64,19,85,062
and write place-value of every digit within the following chart.

We learn the above quantity as thirty-four crore, nineteen lakh,
seventy-five thousand, fifty-two.

Solved Examples Place-value
of a Digit in a Quantity:

1. Write the place-value of 5 within the given numbers:

(i) 50,21,38,761

(ii) 82,05,36,401

(iii) 79,46,15,380

Resolution:

Allow us to prepare the digits within the place-value chart

(i) 

Place worth of 5 within the quantity is

5 × 10,00,00,000 = 50,00,00,000. It’s learn as fifty crore.

(ii)

Place worth of 5 within the quantity is

5 × 1,00,000 = 5,00,000. It’s learn as 5 lakh.

(iii)

Place worth of 5 within the quantity is

5 × 1,000 = 5,000. It’s learn as 5 thousand.

2. Write the place worth of underlined digits within the given clean.

(i) 5,103

(ii) 7,00,496

(iii) 8,15,924

(iv) 2,18,951

Resolution:

(i) 5,103

3 being at one’s or unit’s place

The place worth of three within the quantity 5,103 is 3.

(ii) 7,00,496

7 being at Lakhs-place

The place worth of seven within the quantity 7,00,496 is 7,00,000.

(iii) 8,15,924

2 being at Tens-place

The place worth of two within the quantity 8,15,924 is 20.

(iv) 2,18,951

2 being at Lakhs-place

The place worth of two within the quantity 2,18,951 is 2,00,000.

3. Circle the next.

(i) Digit at lakhs place – 17,45,015

(ii) Digit with face worth of 9 – 49,00,781

(iii) Digit at ten crores place – 92,15,55,470

(iv) Digit at ten 1000’s place – 75,19,778

(v) Digit at tens place – 92,15,55,470

Resolution:

(i) 7

(ii) 9

(iii) 9

(iv) 1

(v) 7

4. Discover the
place worth of 9 within the given numbers.

(i)
6,96,242

(ii)
3,29,162

(iii) 4,52,921

We first
prepare the digits of the given quantity within the place worth chart.

(i) Place worth of 9 within the quantity 6,96,242 is

                   9 × 10,000 = 90,000

 

(ii) Place worth of 9 within the quantity 3,29,162 is

                   9 × 1,000 = 9,000

 

(iii) Place worth of 9 within the quantity 4,52,921 is

                   9 × 100 = 900

5. Write the place worth of the digit underlined in every
quantity.

(i) 67843

(ii) 765432

(iii) 865409

(iv) 736524

(v) 800026

Reply:

5. (i) 7000

(ii) 700000

(iii) 5000

(iv) 30000

(v) 20

6. Rewrite utilizing the Indian place-value chart and write the
quantity identify.

(i) 364,875

(ii) 42, 760, 542

(iii) 6,521,324

Reply:

6. (i) 3,64,875; Three lakh sixty-four thousand eight hundred seventy-five.

(ii) 4,27,60,542; 4 crore twenty-seven lakh sixty thousand 5 hundred forty-two

(iii) 65,21,324; Sixty-five lakh twenty-one thousand 300 twenty-four.

7. Rewrite utilizing the Worldwide place-value chart and
write the quantity identify.

(i) 7,24,60,542

(ii) 21,56,324

(iii) 2,83,964

Reply:

7. (i) 72,460,542; Seventy-two million 4 hundred sixty thousand 5 hundred and forty-two.

(ii) 2,156,324; Two million 100 fifty-six thousand 300 and twenty-four.

(iii) 283,964; 2 hundred eighty-three thousand 9 hundred and sixty-four.

Math Solely Math relies
on the premise that youngsters don’t make a distinction between play and
work and be taught finest when studying turns into play and play turns into
studying.

Nevertheless, options for additional enchancment, from all quarters could be drastically appreciated.

Associated Idea 

4th Grade Math Actions

From Place Worth and Face Worth to HOME PAGE