The amount of a sphere is how a lot area the sphere occupies. Within the determine under, discover that the sphere on the left occupies much less area than the sphere on the fitting. Subsequently, the sphere on the left has much less quantity. 

Quantity of a sphere method

Given the radius, the quantity will be discovered by utilizing the next method:

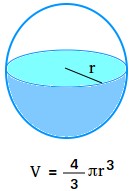
V = (4/3)pir³ = (4/3)πr³

pi or π is a particular mathematical fixed, and it’s roughly equal to 22/7 or 3.14.

If r or the radius of the sphere is understood, the quantity is 4 thirds the product of pi and the dice of the radius of the sphere. 

Suppose the diameter is given as a substitute of the radius. For the reason that radius is half of the diameter, simply divide the diameter by 2 to get the radius earlier than in search of the quantity.

Should you should use the diameter, V = (4/3)π(d/2)³ = (4/3)π(d³/8) = 4πd³/24 = πd³/6

The amount is expressed in cubic models.

• If r is measured in meters, then the quantity is measured in cubic meters or m³.

• If r is measured in centimeters, then the quantity is measured in cubic centimeters or cm³. 

• If r is measured in inches, then the quantity is measured in cubic inches or in.³

Some examples displaying how you can get the quantity of a sphere

Instance #1

Discover the quantity of a sphere that has a radius of two inches

Quantity = 4/3 × π × r³

Quantity = 4/3 × 3.14 × 2³

Quantity = 4/3 × 3.14 × 8

Quantity = 4/3 × 25.12

Quantity = 4/3 × 25.12 / 1

Quantity = (4 × 25.12)/(3 × 1)

Quantity = (100.48) / 3

Quantity = 33.49 cubic inch = 33.49 in.³

Instance #2

Discover the quantity of a sphere with a radius of three ft

Quantity = 4/3 × π × r³

Quantity = 4/3 × 3.14 × 3³

Quantity = 4/3 × 3.14 × 27

Quantity = 4/3 × 84.78

Quantity = 4/3 × 84.78/1

Quantity = (4 × 84.78)/(3 × 1)

Quantity = (339.12)/3

Quantity = 113.04 ft³ = 113.04 cubic ft

Instance #3

Discover the quantity of a sphere of radius 2/3 cm

Quantity = 4/3 × π × r³

Quantity = 4/3 × 3.14 × (2/3)³

Quantity = 4/3 × 3.14 × 2/3 ×2/3 × 2/3

Quantity = 4/3 × 3.14 × 8/27

Quantity = 4/3 × 3.14/1 × 8/27

Quantity = (4 × 3.14 × 8) / ( 3 × 1 × 27 )

Quantity = (100.48)/(81)

Quantity = 1.24 in.³

Quantity of a hole sphere

Suppose a sphere with an interior radius r is faraway from a sphere with an outer radius R. What you find yourself with is known as a hole sphere or a sphere that has a cavity inside it. Within the determine under, the cavity is proven in pink. 

The amount of the cavity is the quantity of the sphere that’s eliminated.

The amount of the hole sphere is no matter is left after the quantity of the cavity is eliminated. That is proven with the aquamarine shade.

Quantity of the hole sphere = quantity of the entire sphere – quantity of the cavity.

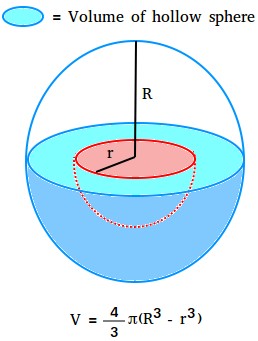
Quantity of hole sphere = (4/3)πR³ – (4/3)πr³

Issue out (4/3)π  

Quantity of hole sphere = (4/3)π(R³ – r³)

Quantity of a hemisphere

A hemisphere is half a sphere. To seek out the quantity of a hemisphere, simply divide the method to search out the quantity by 2.

V = [(4/3)πr³]/2

V = (2/3)πr³

The amount of a hemisphere is 2 thirds the product of pi and the dice of the radius of the sphere. 

Quantity of a sphere utilizing the circumference of a sphere

C  = 2πr

V = (4/3)πr³ 

r = C/2π

V = (4/3)π(C/2π)³

V = (4/3)π(C³/8π³)

V = (4πC³)/(24π³)

V = (4πC³)/(4π)(6π²)

Cancel 4π

V = (C³)/(6π²)

What’s the quantity of the earth?

The earth is a sphere with a radius of 6356 kilometers or 3958.8 miles. What’s the quantity of the earth in cubic miles?

Quantity of the earth = 4/3 × π × 3958.8³

Quantity of the earth = 4/3 × 3.14 × 3958.8 ×3958.8 × 3958.8

Quantity of the earth = 4/3 × 3.14 × 62042699345.5

Quantity of the earth = 4/3 × 194814075945

Quantity of the earth = 4/3 × 194814075945/1

Quantity of the earth = (4 × 194814075945)/(3 × 1)

Quantity of the earth = (779256303779)/(3)

Quantity of the earth = 259,752,101,260 cubic miles

The earth has roughly a quantity of 260 trillion cubic miles.

Derivation of the quantity of a sphere

We want calculus, particularly the idea of integration, with a view to derive the quantity of a sphere or to indicate you a proof. Check out the sphere under and examine it fastidiously!

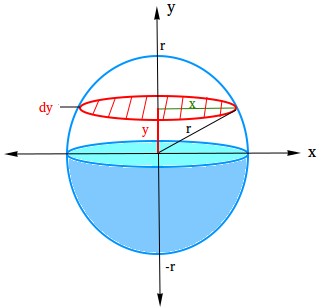
• The pink circle is a skinny disc. Consider it as a really flat cylinder!
• x is the radius of the skinny disc
• dy is the thickness of the skinny disc
• r is the radius of the sphere
• y is the gap from the x-axis to the disc.

Utilizing the Pythagorean theorem, r² = x² + y²

x² = r² – y²

The amount of the skinny disc at that particular peak is πx²dy

Substitute r² – y² for x² in πx²dy

V = π(r² – y²)dy

The whole quantity of the sphere is discovered by including the volumes of all disks for all attainable heights you possibly can put these disks contained in the sphere.

All of the attainable heights are between -r and r (-r ≤ y ≤ r)

The signal that you simply see bellow is the integral image and it a summation, that means so as to add every little thing.

$$ int_{}^{}
$$

The one under means so as to add every little thing from -r ro r

$$ int_{-r}^{r}
$$

The one under means so as to add collectively the volumes of all disks for all attainable heights you possibly can put these disks (-r ≤ y ≤ r).

$$ int_{-r}^{r} π(r^2 – y^2) ,dy $$

In response to linearity rule, you possibly can transfer pi exterior the integral signal.

$$ π int_{-r}^{r} (r^2 – y^2) ,dy $$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = π[yr^2 – frac {y^3}{3} ]_{-r}^
{r} $$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = π[(r^3 – frac {r^3}{3} – (-r^3 – frac {-r^3}{3} )]
$$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = π[( frac {2r^3}{3} – ( frac {-2r^3}{3} )]
$$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = π[( frac {2r^3}{3} + ( frac {2r^3}{3} )]
$$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = π( frac {4r^3}{3})
$$
$$ π int_{-r}^{r} (r^2 – y^2) ,dy = (frac{4}{3}πr^3)
$$