
[ad_1]
The ambiguous case of the regulation of sines occurs when two sides and an angle reverse one of many two sides are given. We will shorten this case with SSA.
For the reason that size of the third facet shouldn’t be identified, we do not know if a triangle will probably be shaped or not. That’s the reason we name this case ambiguous.
In reality, this type of scenario or SSA may give the next 4 eventualities.
The primary state of affairs of the ambiguous case of the regulation of sines happens when a < h.
For instance, check out the triangle under the place solely two sides are given. These two given sides are a and b. An angle reverse to at least one facet can be given. Angle A is the angle that’s reverse to facet a or one of many two sides.
Notice that SSA on this case means facet a facet b angle A in that order.
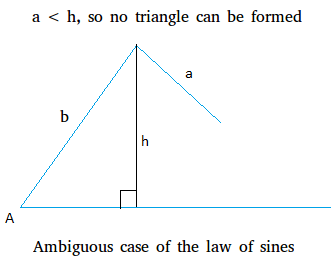
As a result of a is shorter than h, a shouldn’t be lengthy sufficient to type a triangle. In reality, the variety of potential triangles that may be shaped within the SSA case is dependent upon the size of the altitude or h.
h
b
When you multiply each side of the equation above by b, we get h = b sin A.
An instance exhibiting that no triangle might be shaped
Methodology #1
Suppose A = 74°, a = 51, and b = 72.
h = 72 × sin (74°) = 72 × 0.9612 = 68.20
Since 51 or a is lower than h or 69.20, no triangle will probably be shaped.
Methodology #2
We will additionally present that no triangle exists through the use of the regulation of sines.
a / sin A = b / sin B
The ratio a / sin A is thought since a / sin A = 51 / sin 74°
Since we additionally know the size of b, the lacking amount within the regulation of sines is sin B. It’s logical then to search for sin B and see what we find yourself with.
51 / sin 74° = 72 / sin B
51 sin B = 72 sin 74°
sin B = (72 sin 74°) / 51
sin B = (72 × 0.9612) / 51
sin B = (69.2064) / 51
sin B = 1.3569
For the reason that sine of an angle can’t be greater than 1, angle B doesn’t exist. Due to this fact, no triangle might be shaped with the given measurements.
The second state of affairs of the ambiguous case of the regulation of sines happens when a = h.
When a = h, the ensuing triangle will at all times be a proper triangle.
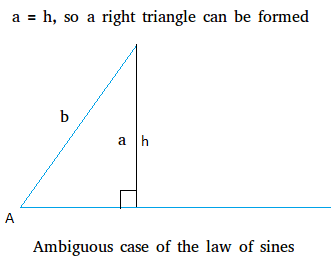
An instance exhibiting {that a} proper triangle might be shaped
Methodology #1
Suppose A = 30°, a = 25, and b = 50.
h = 50 × sin (30°) = 50 × 0.5 = 25
Since 25 or a is the same as h or 25, 1 proper triangle will probably be shaped.
Methodology #2
Once more, we are able to use the regulation of sines to point out that this time sin B exists and it is the same as 90 levels.
a / sin A = b / sin B
25 / sin 30° = 50 / sin B
25 sin B = 50 sin 30°
sin B = (50 sin 30°) / 25
sin B = (50 × 0.5) / 25
sin B = (25) / 25
sin B = 1
B = sin-1(1) = 90 levels.
The third state of affairs of the ambiguous case of the regulation of sines happens when a > h and a > b.
When a is greater than h, once more a triangle might be shaped. Nevertheless, since a is greater than b, we are able to solely have one triangle. Attempt to make a triangle the place a is greater than b, you’ll discover that there can solely be 1 such triangle.
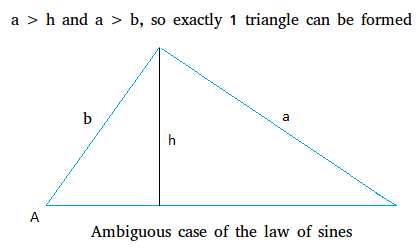
An instance exhibiting that precisely 1 triangle might be shaped
Suppose A = 30°, a = 50, and b = 40.
h = 40 × sin (30°) = 40 × 0.5 = 20
Since 50 or a is greater than each h (or 20) and b (or 40), 1 triangle will probably be shaped.
Final scenario: a > h and a < b
When a is lower than b, 2 triangles might be shaped as clearly illustrated under. The 2 triangles are triangle ACD and triangle AED.
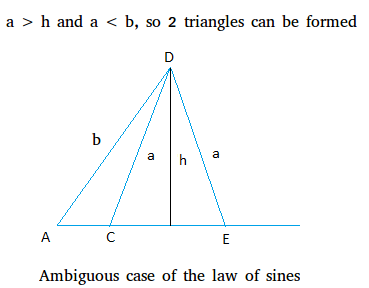
An instance exhibiting that precisely 2 triangles might be shaped
Suppose A = 30°, a = 40, and b = 60
h = 60 × sin (30°) = 60 × 0.5 = 30
Since 40 or a is greater than h and a is smaller than b or 60, 2 triangles will probably be shaped.
[ad_2]