Summary

“Arithmetic is the native language of nature.” is a phrase that’s usually used in the case of explaining why arithmetic is throughout in pure sciences, particularly in physics. What does that imply? A better look exhibits us that it primarily implies that we describe nature by differential equations, plenty of differential equations. There are such a lot of that it might take a complete encyclopedia to collect all of them in a single e-book. The next article is meant to take the reader by means of this maze together with examples, many photos, a bit of little bit of historical past, and the theorem in regards to the existence and uniqueness of options: the theory of Picard-Lindelöf.

A Glimpse of Our Descriptions of the World

All of it started with Isaac Newton in 1687, or if we’re choosy, with Gottfried Leibniz throughout his keep in Paris 1672-1676. The reference to Paris is greater than a facet word since will probably be particularly French mathematicians who will develop the sector of study within the following centuries to the state we all know in the present day. Joseph-Louis Lagrange, Pierre-Simon Laplace, Adrien-Marie Legendre, Augustin-Louis Cauchy, and Pierre-Alphonse Laurent are names we take as a right in on a regular basis use. Charles Briot and Jean-Claude Bouquet coined the time period of a holomorphic operate in 1875 and the household of differential equations
$$
x^my’=f(x,y)
$$
carry their identify. Different nice contributors have been the Bernoulli household (Jakob, Johann, Daniel), Carl-Friedrich Gauß, George Gabriel Stokes, Marius Sophus Lie, and Amalie Emmy Noether to call just a few. All of them set milestones in arithmetic and paved the best way.

In fact, there was essential arithmetic earlier than the seventeenth century, as there was essential physics earlier than Newton. Euclid of Alexandria and Archimedes of Syracuse lived within the third century B.C.! But when we take a look at the principle topics that we’d like in the present day to explain nature, then we are going to find yourself with energy collection and forces.

Physics

All of it started with Isaac Newton in 1687.
$$
F ;sim;ddot{x}
$$
is these days the definition of a pressure. And it’s a differential equation! The equation additionally tells us what occurs with out a pressure, specifically that there is no such thing as a change of movement ##dot{v}## both, i.e. movement is conserved beneath the absence of forces
$$
F =0;Longleftrightarrow ;ddot{x}=dot{v}=0.
$$
Emmy Noether [1],[2] confirmed 231 years later that each conserved bodily amount corresponds to invariants of differential expressions. For instance, James Clerk Maxwell launched in 1864 his equations of electromagnetism that are all differential equations. Electromagnetism is a principle of the corresponding vector fields.
start{align*}
vec{nabla} instances vec{H}=vec{j}+dot{vec{D}}; &, ;
vec{nabla} instances vec{E}=-dot{vec{B}}
vec{nabla} cdot vec{D}=rho; &, ;
vec{nabla} cdot vec{B}=0
finish{align*}
Albert Einstein [3] even described the entire cosmos in 1915 by the differential Einstein Discipline Equations
$$
R_{mu nu }-{frac{1}{2}}g_{mu nu }R+Lambda g_{mu nu }={frac{8pi G}{c^{4}}}T_{mu nu }.
$$
These are excellent outcomes with none doubt. The instance of forces in classical, say non-relativistic physics and Noether’s theorem, nonetheless, present that there are extra examples to anticipate.

What the Taylor collection is for mathematicians
$$
f(x)=sum_{n=0}^infty dfrac{(x-x_0)^n}{n!}cdot left. dfrac{d^n}{dx^n}proper|_{x=x_0}f(x)
$$
is the harmonic oscillator for physicists
$$
{ddot{x}}+omega^{2},x=0.
$$
They seem yearly in the course of the research of arithmetic, resp. physics in new variations and contexts, and each are differential expressions. Balthasar van der Pol present in 1927 whereas finding out vacuum tubes an oscillator with non-linear damping and constructive suggestions
$$
ddot{x}-varepsilon (1-x^{2}){dot{x}}+x=0
$$
that doesn’t enable a closed resolution. Most programs aren’t as good as waves
$$
ddot{x}sim nabla^2 x
$$
or the warmth equation (Jean-Baptiste Joseph Fourier, 1822)
$$
dot{x}simnabla^2 x.
$$
The holy grail of differential equation programs among the many not-so-nice programs are the Navier-Stokes equations
$$
{displaystyle overbrace {underbrace {frac {partial mathbf {u} }{partial t}} _{start{smallmatrix}{textual content{Variation}}finish{smallmatrix}}+underbrace {(mathbf {u} cdot nabla )mathbf {u} } _{start{smallmatrix}{textual content{Convection}}finish{smallmatrix}}} ^{textual content{Inertia (per quantity)}}overbrace {-underbrace {nu ,nabla ^{2}mathbf {u} } _{textual content{Diffusion}}=underbrace {-nabla w} _{start{smallmatrix}{textual content{Inside}}{textual content{supply}}finish{smallmatrix}}} ^{textual content{Divergence of stress}}+underbrace {mathbf {g} } _{start{smallmatrix}{textual content{Exterior}}{textual content{supply}}finish{smallmatrix}}}.
$$
They’re named after Claude Louis Marie Henri Navier and George Gabriel Stokes, they usually describe the habits of fluids and gases like water, air, or oil. They’re subsequently essential within the growth and design of ships, airplanes, and automobiles. They’ll solely be solved numerically of their discrete model. There are not any precise analytical options for these difficult purposes. The Navier-Stokes equations are additionally a mathematical problem as a result of we have no idea whether or not there’s an everywhere-defined, easy, and distinctive resolution for the final three-dimensional case in any respect. This is without doubt one of the seven-millennium prize issues [4]. The Poincaré conjecture is taken into account to be solved by Grigori Perelman (2002,2003) so we should always most likely higher communicate of the six-millennium prize issues of the Clay Arithmetic Institute.

The language of physics, a minimum of the facet of it with which we’re involved, specifically differential geometry, is filled with designations for differential expressions. There may be in fact the straightforward differentiation that results in the differential operator
$$
dfrac{d}{dx}
$$
The purpose why it carries its personal identify apart from differentiation is the viewpoint: we remodel one operate ##xmapsto f(x)## to a different operate ##xmapsto f'(x)## reasonably than computing slopes. Its multivariate counterpart is the Nabla operator
$$
vec{nabla }=left({dfrac{partial }{partial x_{1}}},ldots ,{dfrac{partial }{partial x_{n}}}proper)$$
that produces the gradient vector of a operate. It results in the Laplace operator
$$
Delta f=nabla cdot (nabla f)=(nabla cdot nabla )f=nabla^{2}f
$$
when utilized twice. It deserves its personal identify because it seems in one other designation, the Schrödinger operator
$$
dfrac{hbar^{2}}{2m}Delta +V
$$
and the d’Alembert operator
$$
Field=dfrac{1}{c^2}dfrac{partial^2}{partial t^2} -Delta ,.
$$
Even the Hodge star operator
$$
{}^ast colon Lambda ^{ok}(V^{*})rightarrow Lambda ^{n-k}(V^{*})
$$
that solely transforms vectors in Graßmann algebras, at first sight, is an operator between cotangent areas at second sight and thus an operator in differential geometry, too. There are additionally named differential equations or higher, differential formalisms that carry particular names just like the Lagrangian or Euler-Lagrange equation
$$
dfrac{d}{dt}dfrac{partial L}{partial dot{q}}- dfrac{partial {L}}{partial q}=0
$$
The significance of differential expressions within the description of physics is mirrored within the language of physics. Nonetheless, I promised you the outline of the world and though we already had the outline of the cosmos, and physics is per definition all of nature, let’s take a look into different fields of science.

Different Sciences

We discover differential equations even in Chemistry which is by nature a discrete world, e.g. the response equation of three substances [5]
$$
dot{x}(t)=Ok(A-x)(B-x)(C-x)
$$
This seems admittedly a bit synthetic however differential equations have been actually fashionable in 1889. And to be truthful, the steadiness equation in a Bachelor’s paper from 2010 [6] in chemistry just isn’t a lot of a distinction. My professor for differential programs used to say that the whole world is discrete should you solely look intently sufficient. However, he taught us how differential equation programs may be approached and in some circumstances solved. So differential equation programs discovered their method even into chemistry.

The state of affairs adjustments fully as quickly as we take into account stochastic differential equations, i.e. derivatives of chance density capabilities ##P(x,t).## This opens up the door for a complete number of purposes, particularly in economics. The Fokker-Planck differential equations named after Adriaan Daniël Fokker and Max Planck
$$
dfrac{partial }{partial t}P(x,t)=underbrace{-dfrac{partial }{partial x}left[A(x,t)P(x,t)right]}_{textual content{drift}}+underbrace{dfrac{1}{2}dfrac{partial^2 }{partial x^2}left[B(x,t)P(x,t)right]}_{textual content{diffusion / fluctuation}}
$$
are extensively utilized in economics, e.g., in foreign currency trading [7], equilibrium fashions for insider buying and selling [30], on transition processes of revenue distributions [8], and extra. The associated Black-Scholes differential equations
$$
dfrac{partial C(x,t)}{partial t}=-dfrac{1}{2}sigma^2x^2 dfrac{partial^2 C(x,t)}{partial x^2}-rxdfrac{partial C(x,t)}{partial x}+rC(x,t)
$$
named after Fischer Black and Myron Samuel Scholes are thought of a milestone in possibility prizing [9]; ##C(x,t)## represents the prize of the derivatives. One other instance of differential equations in economics is Kaldor’s development mannequin [10] from 1957 named after Káldor Miklós
$$
dot{y} sim c(y) +dot{ok} – y +k_0
$$
the place ##y## is the gross nationwide revenue, and ##ok## the nationwide capital inventory. Even automotive visitors may be modeled by differential equations, the visitors equation, a non-linear hyperbolic wave equation for movement ##f(x,t)## and density ##varrho(x,t)##
$$
dfrac{partial }{partial t}varrho(x,t) + dfrac{partial }{partial varrho}f(varrho (x,t))cdot dfrac{partial }{partial x}varrho(x,t)=0,.
$$
In fact, economics, macro- in addition to microeconomics additionally use the extensive areas of sport principle [11], and control-theory [12],[13]. Differential equation programs play a central position in each fields. Let me point out the mean-field sport principle for example. It’s the research of strategic decision-making by small interacting brokers in massive populations.
start{align*}
partial u_t-nu Delta u+H(x,m,Du)&=0{partial m_t}-nu Delta m-operatorname{div}(D_{p}H(x,m,Du)m)&=0 u(x,T)-G(x,m(T))&=0
finish{align*}
The same identify to mean-field principle in physics is meant.

An usually missed software of differential equation programs is timber administration, on native in addition to nationwide ranges. The timber business is nearly predestined for differential equations: long-term investigation durations, pure development with human disturbances, and yield optimization beneath constraints. D.B. Müller launched a regional mannequin that he known as XYLOIKOS in his Dissertation [14] that’s based mostly on ##200## years of information. His customary model of the mannequin consists of ##221## coupled non-linear integral and differential equations, ##182## parameter capabilities, and ##371## single parameters! The corresponding simulation has been realized H.P. Bader and R.Scheidegger in Rocky-Mountain-Fundamental, 1996 [15].

Contemplating the complexity of differential equation programs within the regional timber business, think about the scale of local weather fashions! I like to recommend that readers search for lecture notes on college servers, e.g. [16], and the literature talked about there. The primary normal circulation mannequin by Manabe and Wetherald dates again to 1967 [17], and we’ve got been progressing ever since. We are able to’t even come near going into local weather fashions right here, so I simply wish to point out Daisyworld – with a blinking eye.

start{align*}
dot{A}_w&=left(beta_wA_g – chi proper)A_w
dot{A}_b&=left(beta_bA_g – chi proper)A_b
A_g&=1-A_w-A_b
finish{align*}
James Lovelock and Andrew Watson created a pc simulation in 1983 [18] so as to help the Gaia paradigm which says that the biosphere of a planet, our planet, types a synergistic and self-regulating, complicated system that helps to take care of and perpetuate the situations for all times on a planet. Their hypothetical planet had solely two life types, black and white daisies, and is in any other case just like Earth [19]. They primarily investigated the scale of the areas the place these daisies develop and their albedo impact. Each, the Gaia paradigm in addition to the simplifications of the mannequin had been topic to criticism and we should not overlook the time, will say, the elevated laptop capability we gained within the meantime.

An ideal second to recollect Moore’s regulation: the variety of transistors on microchips doubles each two years [20].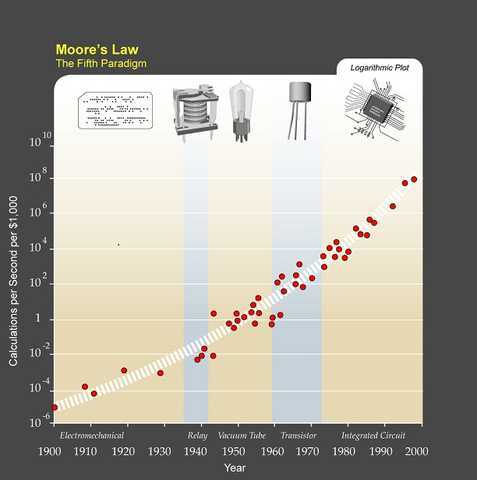

Biology

Any differential expression is a formulation about change, usually based on a time variable. And biology is the sector of pure sciences the place all is about change, specifically development.
$$
dot{x}sim x
$$
is the only and most elementary formulation of development. Its resolution is
$$
tlongmapsto x(t)=e^{at}
$$
and subsequently known as exponential development, cp. [21]. It describes for instance the unconstrained development of micro organism, or Moores’s regulation. Nonetheless, nothing in nature is with out constraints. We take into account thus in a primary step the logistic development
$$
dot x sim xcdot (c-x)
$$
with a capability restrict, e.g. the scale of the Petri dish. However apart from a bacterium in a Petri dish are micro organism within the wild not impartial from one other, or different altering parameters. This implies, that the higher we wish to describe actuality, the extra we’ve got to contemplate coupled programs with suggestions, be it constructive (virus an infection) or damaging (declining sources). The earlier examples confirmed this. One of many extra well-known lessons of differential equation programs in nature are SIR or Kermack-McKendrick-models, particularly with Covid in thoughts [22],[23]
start{align*}
dfrac{mathrm{d} S}{mathrm{d} t}&=nu ,N-beta dfrac{S,I}{N}-mu ,S;,[6pt]
dfrac{mathrm{d} I}{mathrm{d} t}&=beta dfrac{S,I}{N}-gamma ,I-mu ,I;,[6pt]
dfrac{mathrm{d} R}{mathrm{d} t}&=gamma ,I-mu ,R;.
finish{align*}

SIR fashions are supposed to explain outbreak, course, and the top of epidemics and pandemics and had been launched by William Ogilvy Kermack and Anderson Grey McKendrick in 1927 [24]. The three portions into consideration are the variety of Susceptible people, the variety of Infectious people, and the variety of Removed (and immune) or deceased people. The extensions of the mannequin that additionally take the variety of Exposed people under consideration are known as SEIR fashions [25]. The coefficients replicate restoration and an infection charges, and normal beginning and loss of life charges. They don’t rely upon time, which is a big simplification in comparison with real-life pandemics the place various forms of a virus happen.

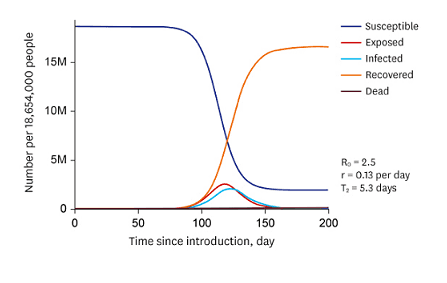
Predator-Prey Mannequin

The differential equations for a system with a predator and a prey inhabitants have been arrange independently by Alfred James Lotka [26] in 1925 and Vito Volterra [27] a yr later. The Lotka-Volterra fashions work fairly nicely for 2 or three species. Moreover, they’ve the massive benefit that we will draw, clarify, clear up – kind of – and take a look at them. That’s why they present up in each textbook that offers with coupled differential equation programs and consequently, right here, too. The essential thought behind the equations is, and it is a well-documented phenomenon in numerous organic conditions, {that a} inhabitants of predators thrives when prey is there in abundance, which declines the inhabitants dimension of prey, in order that predators are pressured to have fewer offspring, and the inhabitants of prey can recuperate till the cycle begins once more. The 2 coupled differential equations are
start{align*}
dot{x}(t)&=x(t)left(alpha -beta y(t)proper)
dot{y}(t)&=-y(t)left(gamma -delta x(t)proper)
finish{align*}
the place ##t## is the time variable, ##x(t)## the inhabitants dimension of prey, and ##y(t)## the variety of predators. The coefficients are the parameters. They have to be adjusted to the state of affairs beneath investigation. ##alpha >0## is the beginning fee of prey on ideally suited situations, ##beta>0## the loss of life fee per predator. ##gamma >0## is the loss of life fee amongst predators, and ##delta ## the replica fee of predators per prey. If I bear in mind accurately, then my professor talked about wolves, mountain hares, and caribous in Nova Scotia as a working instance. Nonetheless, will probably be ample for demonstration causes to decide on some fantasy values that guarantee good photos. Therefore we are going to take into account the equations
start{align*}
dfrac{dx(t)}{dt}=dot{x}(t)&=10x(t)-2x(t)y(t)=(10-2y(t))cdot x(t)[6pt]
dfrac{dy(t)}{dt}=dot{y}(t)&=-7y(t)+x(t)y(t)=(-7+x(t))cdot y(t)
finish{align*}
If we remove ##dt## and combine on either side, then
$$
y(t)^{10}e^{-2y(t)}=kcdot x(t)^{-7}e^{x(t)}, , ,ok=e^C>0
$$
which transforms to the operate
$$
F(x,y)=dfrac{e^{x}}{x^7}cdot dfrac{e^{2y}}{y^{10}} =dfrac{1}{ok}=e^{-C}
$$
Though we nonetheless have no idea what ##x(t),y(t)## seem like, we already can conclude just a few properties of the system. If we differ the fixed ##ok## and plot the graph of ##F(x,y)##, then we get the section plot or section area plot of the Lotka-Volterra system,

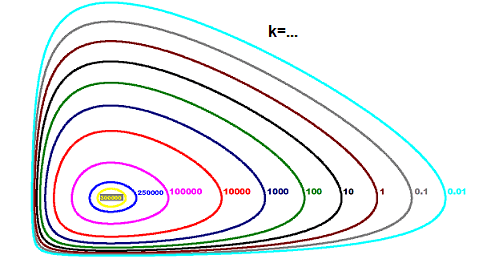
The three-dimensional graph of ##F(x,y)## seems a bit like a bowl [28].

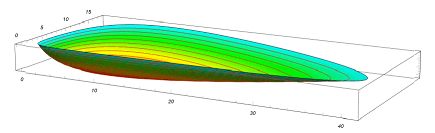
It consists of all potential flows ##F(x,y)=1/ok##

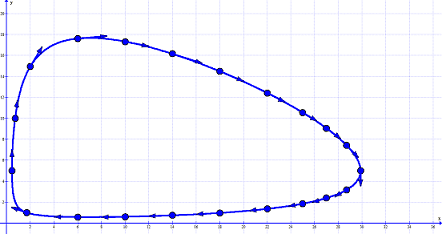
by means of the vector subject of the differential equation system

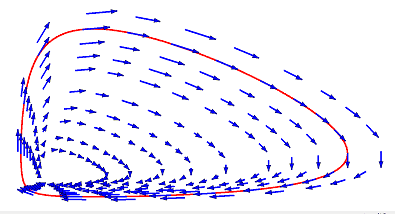
The diagrams present us that

1. Not one of the two populations can turn out to be extinct.
2. Each inhabitants sizes differ periodically by time for the reason that flows are closed curves. We already anticipated this from the casual description.
3. Which movement of all potential ones is the precise one relies upon solely on the preliminary values of the system, e.g. the purple line by means of the vector subject.
4. There have to be a important level at some massive worth of ##ok.##
   start{align*}
   F_x=dfrac{partial F}{partial x}&=left(dfrac{1cdot e^x}{x^7}-7dfrac{e^x}{x^8}proper)cdot dfrac{e^{2y}}{y^{10}}=dfrac{(1cdot x- 7)e^x}{x^8}cdot dfrac{e^{2y}}{y^{10}}
   F_y=dfrac{partial F}{partial y}&=left(dfrac{2cdot e^{2y}}{y^{10}}-10dfrac{e^{2y}}{y^{11}}proper)cdot dfrac{e^{x}}{x^{7}}=dfrac{(2cdot y- 10)e^{2y}}{y^{11}}cdot dfrac{e^{x}}{x^{7}}[6pt]
   F_x=0 &Longleftrightarrow x_0=dfrac{gamma }{delta }=7
   F_y=0 &Longleftrightarrow y_0=dfrac{alpha}{beta}=5
   finish{align*}
   We have now subsequently a important level at ##(7,5)## which is an area minimal. It corresponds to ##kapprox 332,951## and ##Capprox 12.7.##
5. Assume that ##T## is the widespread interval of each populations. Then
   start{align*}
   0&=log x(T) -log x(0)=int_0^T dfrac{d}{dt}(log x(t)),dt=int_0^T (alpha – beta cdot y(t)),dt&=alpha T-betaint_0^Ty(t),dt =10-2int_0^Ty(t),dt
   finish{align*}
   and the imply inhabitants dimension of predators is
   $$
   MV(y) = dfrac{1}{T}int_0^T y(t),dt = dfrac{alpha}{beta}=5=y_0
   $$
   and analog for the imply inhabitants dimension of prey
   $$
   MV(x) = dfrac{1}{T}int_0^T x(t),dt = dfrac{gamma }{delta }=7=x_0
   $$
   The imply inhabitants sizes of predator and prey are solely depending on the important level. They’re particularly impartial of the preliminary values of the system, i.e. equal for any particular resolution aka movement.
6. The periodic inhabitants sizes are irregular within the sense that we solely get pure sines and cosines if the flows are elliptic or a circle.
   finish{enumerate}
   We have now thus realized rather a lot in regards to the state of affairs with out really fixing it. This may be performed numerically by linearization, i.e. working with small variations as an alternative of differentials. The end result [29] in our case is by the Runge-Kutta-Fehlberg technique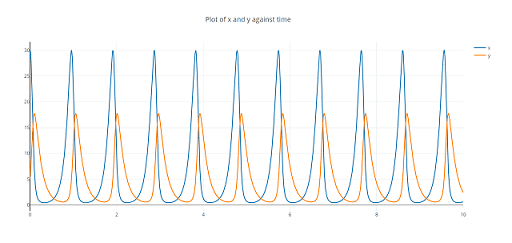
   

Attractors, Repellers, and Unusual Attractors

We have now seen that vector fields, like ##(F_x,F_y)## above, are good prospects for analyzing differential equation programs. We are able to draw them comparatively simply as linear, i.e. first-order approximations they usually inform us the course of flows, i.e. options. Two phenomena are particularly of curiosity: attractors and repellers. 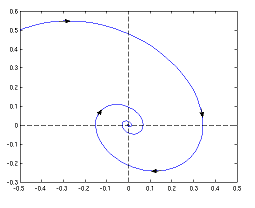An attractor is a area the place a movement can’t escape from as soon as it’s inside, ##F(t,A)subseteq A.## If an attractor is some extent [31], then flows converge to such some extent.

A repeller is a damaging attractor, a area or level the place flows run away from. Switching the instructions of the vectors that type an attractor generates a repeller. A magnetic subject with its subject traces is an efficient creativeness of what attractors and repellers are. In fact, complicated vector fields can have each of them and multiple, too. A charged particle is attracted from one facet of a dipole and repelled from the opposite.

Edward Norton Lorentz, a US-American meteorologist, and mathematician investigated an idealistic hydrodynamic system to foretell states of the ambiance and located 1963 a strange-looking attractor [32] of
start{align*}
dot X&=a(Y-X)
dot Y&=X(b-Z)-Y
dot Z&=XY-cZ,.
finish{align*}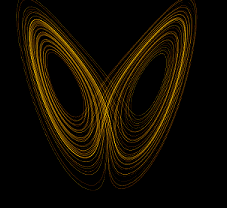
We subsequently communicate of unusual attractors and the one above is the Lorenz attractor. Different well-known, and unusual attractors are the (Otto) Rössler attractor (1976) [33]
start{align*}
dot X&=-Y-Z
dot Y&=X+aY
dot Z&=b+XZ-cZ,.
finish{align*}
or the (Michel) Hénon attractor for the discrete system
$$
x_{ok+1}=y_{ok}+1-ax_{ok}^{2}; , ;y_{ok+1}=bx_{ok},.
$$

Theorem of Picard-Lindelöf

We take into account a operate (movement) on a compact (time) interval ##Isubseteq mathbb{R}##
$$
u, : ,[a,b] longmapsto mathbb{R}^n
$$
and the preliminary worth drawback (IVP)
start{align*}
dot{u}(t)=f(t,u(t)); , ;u(a)=y_0 qquad ({}^*)
finish{align*}
for a operate ##f, : ,[a,b]instances mathbb{R}^nlongmapsto mathbb{R}^n## and ask for options. The (international model) of the theorem of Picard-Lindelöf (1890) says, that if ##f## is steady, and globally Lipschitz-continuous within the second variable, then there exists a singular differentiable resolution ##overline{u}## of the IVP ##({}^*)## for each ##y_0in mathbb{R}^n,## and the sequence
$$
v_{ok+1}:=y_0 +int_a^t f(s,v_k(s)),dsqquadqquad tin [a,b], , ,kin mathbb{N}_0
$$
converges uniformly to ##overline{u}.##

The thought of the proof is to contemplate the fastened level equation
$$
u(t)=T.u(t)=u_0+int_a^t f(s,u(s)),ds
$$
and show with the assistance of the Lipschitz continuity that for the integral operator ##T## holds
$$
|T.u-T.v|_infty leq Lcdot (b-a)cdot |u-v|_infty ,,
$$
change to a weighted norm
$$
|u|leq |u|_infty leq |u|e^{alpha (b-a)},,
$$
then show that we get pointwise
$$
left|T.u(t)-T.v(t)proper|leq dfrac{b-a}{alpha} cdot |u-v|cdot e^t-a,,
$$
which implies for an acceptable alternative of ##alpha## that
$$
|T.u-T.v|leq dfrac{b-a}{alpha} cdot |u-v| <|u-v|,.
$$
Which means ##T## is a contraction and the end result follows by the Banach fixed-point theorem.##qquad;;;;Field##

It’s apparent that the worldwide Lipschitz situation within the second variable, i.e. the movement and resolution curve is important for the theory. Though the theory remains to be relevant to massive lessons of issues, e.g. the linear case for steady capabilities
start{align*}
dot{u}&=A(t)cdot u + r(t)[6pt]
|f(t,u)-f(t,v)|&leqdisplaystyle{sup_{tin[a,b]}}|A(t)| cdot|u-v|,,
finish{align*}
it’s on the similar time its best weak point. We are able to show an area model of the theory or comparable native statements like the theory of Peano with completely different situations, however we can’t remove the fundamental drawback to maintain the potential flows beneath management with out assuming applicable situations beforehand. That is for my part system immanent and one of many the reason why Navier-Stokes has made it a Millenium Prize Drawback.

We nonetheless would not have a passable reply as as to whether there are undoubtedly arduous issues on this world or whether or not we merely failed to seek out good options.

Sources