[ad_1]
The elemental geometrical ideas depend upon three fundamental ideas — level, line and aircraft. The phrases can’t be exactly outlined. Nonetheless, the meanings of those phrases are defined via examples.
Level:
Take a tremendous pencil and mark a dot with it on paper. Name it P. We are saying that P is some extent.
Thus, a dot represents some extent.
|
● It’s the mark of place and has an actual location. ● It has no size, breadth or thickness. ● It’s denoted by a dot made by the tip of a pointy pencil. ● It’s denoted by capital letter. ● Within the given determine P, Q, R represents completely different factors. |
Line:
● It’s a straight path which might be prolonged indefinitely in each the instructions.
● It’s proven by two arrowheads in reverse instructions.
● It doesn’t have any mounted size.
● It has no endpoints.
● It’s denoted as AB ↔ or BA↔ and is learn as line AB or line within the BA.
● It could possibly by no means be measured.
● Infinite variety of factors lie on the road.
● Generally it’s also denoted by small letters of the English alphabet.
To know the thought of a line, allow us to carry out the next actions:
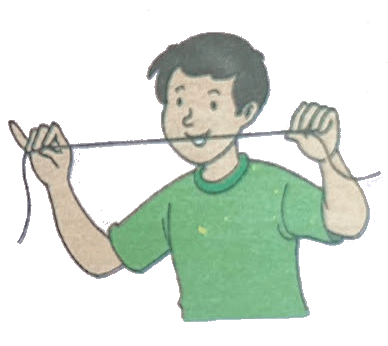
Exercise I:
|
Take a thread. Take one finish of it in a single hand and the opposite finish within the one other hand. Stretch the thread straight. We are saying that it kinds a straight line. |
|
Now, unfastened the thread. What will we observe? The straight thread now turns into curved. This provides the idea of a curved line. |
Exercise II:
|
Take a bit of paper. Fold it alongside the center. Press the fold firmly. Open up the folded paper and observe the crease in the course of the paper. This crease on the paper provides an thought of a straight line. |
|
Examples of Straight Traces |
Examples of curved traces |
|
The sides of a blackboard, the sides of the desk prime, and fringe of a stick are some examples of straight traces. |
Traces obtained by drawing alongside the sting of a bangle, cash and so forth. are examples of curved traces. |
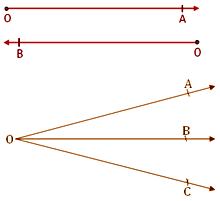
Ray:
● It’s a straight path which might be prolonged indefinitely in a single route solely and the opposite finish is mounted.
● It has no mounted size.
● It has one endpoint referred to as the preliminary level.
● It can’t be measured.
● It’s denoted as OA<span model=”font-size: 50%”>→ and is learn as ray OA.
● Quite a lot of rays might be drawn from an preliminary level O.
● Ray OA and ray OB are completely different as a result of they’re prolonged in several instructions.
● Infinite factors lie on the ray.
Line Phase:
● It’s a straight path which has a particular size.
● It has two endpoints.
● It is part of the road.
● It’s denoted as AB or BA.
● It’s learn as line section AB or line section BA.
● The gap between A and B is named the size of AB.
● Infinite variety of factors lies on a line section.
● Two line segments are mentioned to be equal if they’ve the identical size.
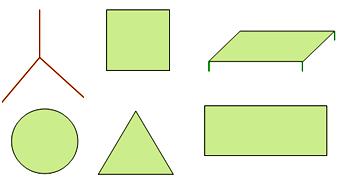
Aircraft:
A easy, flat floor provides us an thought of a aircraft. The floor of the desk, wall, blackboard, and so forth., is easy and flat. It extends endlessly in all of the instructions. It has no size, breadth or thickness. Right here, we now have proven a portion of a specific aircraft. We are able to draw sure figures like sq., rectangle, triangle, and circle on the aircraft. Therefore, these figures are additionally referred to as aircraft figures.
Incidence Properties of Traces in a Aircraft:
● An infinite variety of many traces might be drawn to cross via a given level in a aircraft.
By a given level in a aircraft, infinitely many traces might be drawn to cross via.
● Two distinct factors in a aircraft decide a singular line.
One and just one line might be drawn to cross via two given factors, i.e., two distinct factors in a aircraft. This line lies wholly within the aircraft.
● Infinite variety of factors lie on the road in a aircraft.
● Two traces in a aircraft both intersect at some extent or they’re parallel to one another.
Collinear Factors:
Two or extra factors which lie on the identical line in a aircraft are referred to as collinear factors.
● The road is named the road of colinearity.
● Two factors are at all times collinear.
● Within the adjoining determine………
Factors A, B, C are collinear mendacity on line
Factors X, Y, Z aren’t collinear as a result of all of the three factors don’t lie on a line.
Therefore, they’re referred to as non-collinear factors.
Equally, right here factors M, N, O, P, Q are collinear factors and A, B, C are non-collinear factors.
Be aware:
Two factors are at all times collinear.
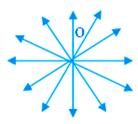
Concurrent Traces:
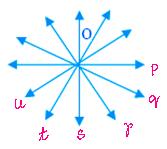
Three or extra traces which cross via the identical level are referred to as concurrent traces and this widespread level is named the purpose of concurrence. Within the adjoining determine, traces p, q, r, s, t, u intersect at level O and are referred to as concurrent traces.
Two traces in a Aircraft:
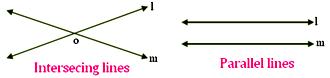
Intersecting Traces: Two traces in a aircraft which lower one another at widespread level are referred to as intersecting traces and the purpose is named the purpose of intersection. Within the adjoining determine, traces l and m intersect at level O.
Parallel Traces: Two traces in a aircraft which don’t intersect at any level, i.e., they don’t have any level in widespread are referred to as parallel traces. The gap between the 2 parallel traces stays the identical all through.
These are the elemental geometrical ideas defined above utilizing figures.
● Traces and Angles
Some Geometric Phrases and Outcomes
Complementary and Supplementary Angles
Parallel and Transversal Traces
From Basic Geometrical Ideas to HOME PAGE
Did not discover what you have been in search of? Or need to know extra data
about Math Solely Math.
Use this Google Search to search out what you want.
[ad_2]