
[ad_1]
The realm method is used to seek out the variety of sq. models a polygon encloses. The determine beneath exhibits some space formulation which can be ceaselessly used within the classroom or within the real-world.
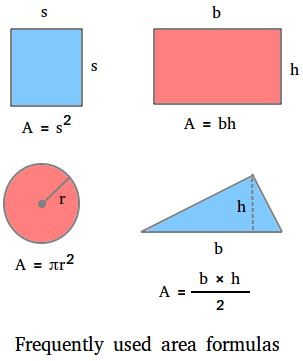
Space of a sq.
The realm of a sq. is the sq. of the size of 1 aspect. Let s be the size of 1 aspect.
A = s2 = s × s
Space of a rectangle
The realm of a rectangle is the product of its base and top.
Let b = base and let h = top
A = b × h = bh
For a rectangle, “size” and “width” may also be used as an alternative of “base” and “top”
The realm of a rectangle may also be the product of its size and width
A = size × width
Space of a circle
The realm of a circle is the product of pi and the sq. of the radius of the circle.
Let r be the radius of the circle and let pi = π = 3.14
A = πr2
Please see the lesson about space of a circle to get a deeper information.
Space of a triangle
The realm of a triangle is half the product of the bottom of the triangle and its top.
Let b = base and let h = top
Space = (b × h)/2
Space of a parallelogram
The realm of a parallelogram is the product of its base and top.
Let b = base and let h = top
A = b × h = bh
Please see the lesson about parallelogram to be taught extra.
Space of a rhombus
The realm of a rhombus / space of a kite is half the product of the lengths of its diagonals.
Let d1 be the size of the primary diagonal and d2 the size of the second diagonal.
A = (d1 × d2)/2
Space of a trapezoid
The realm of a trapezoid is half the product of the peak and the sum of the bases.
Let b1 be the size of the primary base, b2 the size of the second base, and let h be the peak of the trapezoid.
A = [h(b1 + b2)]/2
Please see the lesson about space of a trapezoid to be taught extra.
Space of an ellipse
The realm of the ellipse is the product of π, the size of the semi-major axis, and the size of the semi-minor axis.
Let a be the size of the semi-major axis and b the size of the semi-minor axis.
A = πab
The semi-major axis can be referred to as main radius and the semi-minor axis is named minor radius.
Let r1 be the size of the semi-major axis and r2 the size of the semi-minor axis.
The realm can be equal to πr1r2
A few instance exhibiting the best way to use the realm method
Instance #1
What’s the space of an oblong yard whose size and breadth are 50 toes and 40 toes respectively?
Resolution:
Size of the yard = 50 ft
Breadth of the yard = 40 ft
Space of the yard = size × breadth
Space of the yard = 50 ft × 40 ft
Space of the yard = 2000 sq. toes = 2000 ft2
Instance #2
The lengths of the adjoining sides of a parallelogram are 12 cm and 15 cm. The peak equivalent to the 12-cm base is 6 cm. Discover the peak equivalent to the 15-cm base.
Resolution:
A = b × h = 12 × 6 = 72 cm2
Because the space remains to be the identical, we are able to use it to seek out the peak equivalent to the 15 cm base.
A = b × h
Substitute 72 for A and 15 for b.
72 = 15 × h
Divide each side of the equation by 15
72/15 = (15/15) × h
4.8 = h
The peak equivalent to the 15 cm base is 4.8 cm.
Instance #3
The diameter of a circle is 9. What’s the space of the circle?
Resolution:
Because the radius is half the diameter, r = 9/2 = 4.5
A = πr2
A = 3.14(4.5)2
A = 3.14(20.25)
A = 63.585
[ad_2]