
[ad_1]
In formation of numbers we are going to study the numbers having completely different numbers of digits.
We all know that:
(i) Biggest variety of one digit = 9,
Smallest variety of 2 digits = 10.
(If one is added to 9, we get 9 + 1 = 10).
(ii) Biggest variety of 2 digits = 99,
Smallest variety of 3 digits = 100.
(If one is added to 99, we get 99 + 1 = 100).
(iii) Biggest variety of 3 digits = 999,
Smallest variety of 4 digits = 1000.
(If one is added to 999, we get 999 + 1 = 1000).
(iv) Biggest variety of 4 digits = 9999,
Smallest variety of 5 digits = 10000.
(If one is added to 9999, we get 9999 + 1 = 10000).
(iv) Biggest variety of 5 digits = 99999,
Smallest variety of 6 digits = 100000.
(If one is added to 99999, we get 99999 + 1 = 100000).
Thus, if 1 is added to 9 (best 1-digit quantity), we get 10 (smallest 2-digit quantity).
If 1 is added to 99 (best 2-digit quantity), we get 100 (smallest 3-digit quantity).
If 1 is added to 999 (best 3-digit quantity), we get 1000 (smallest 4-digit quantity).
If 1 is added to 9999 (best 4-digit quantity), we get 10000 (smallest 5-digit quantity).
If we add 1 to 99999, we get 99999 + 1 = 100000, the smallest 6-digit numbers.
|
Variety of Digits |
Smallest Quantity |
Biggest Quantity |
|
One |
0 |
9 |
|
Two |
10 = 9 + 1 |
99 |
|
Three |
100 = 99 + 1 |
999 |
|
4 |
1000 = 999 + 1 |
9999 |
We observe that
● The smallest 2-digit quantity is the
(Biggest 1-digit quantity + 1)
● The smallest 3-digit quantity is the
(Biggest 2-digit quantity + 1)
● The smallest 4-digit quantity is the
(Biggest 3-digit quantity + 1)
● Subsequently,
The smallest 5-digit quantity is the
(Biggest 4-digit quantity + 1)
i.e., 999 + 1 = 10000 (Ten thousand)
We learn 100000 as one lakh. The sixth place from the fitting is known as lakhs place.
For Instance:
500000 –> learn as 5 lakh.
639043 –> learn as six lakh thirty-nine thousand forty-three.
832519 –> learn as eight lakh thirty-two thousand 5 hundred nineteen.
999999 –> learn as 9 lakh ninety-nine thousand 9 hundred ninety-nine.
999999 is the best 6-digit quantity.
Have a look at the next desk:
Now we are going to discover ways to use
an abacus in quantity formation
These details could be expressed on a spike-abacus as
follows:
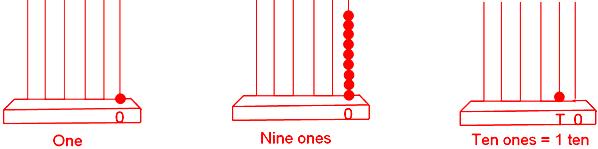
One → 9, 9 + 1 = 10 = One ten
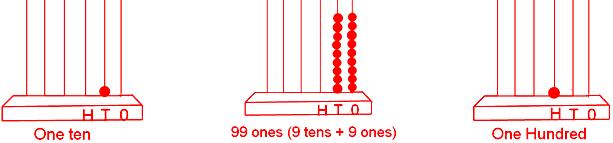
10 → 99, 99 + 1 = 100 = 100

100 → 999, 999 + 1 = 1000 = One thousand
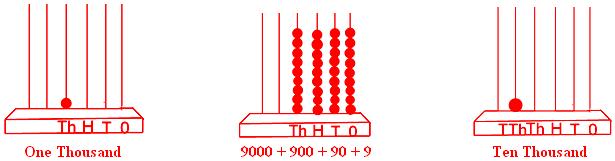
1000 → 9999, 9999 + 1 = 10000 = Ten thousand
1-digit numbers:
1, 2, 3, 4, 5, 6, 7, 8, 9.
2-digit numbers:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, …………., 29,
30, 31, ……., 39, 40, 41,……….., 49, 50, 51,………, 60, 61,………., 69, 70, 71, 72, ……….., 79, 80, 81, ………., 89, 90, 91, ……………………, 99
3-digit numbers:
100, 101, …….., 199, 200, 201, ……, 299, 300, ……., 399, 400, ………, 499,
500, ….., 599, 600, ……, 699, 700, …., 799, 800, 801, ……, 890, ……., 899,
900, 901, ………, 990, 991, ……………, 999.
4-digit numbers:
1000, 1001,……,1099,1100,1101,……,1199,1200,1201,…………,1299,
1300, ……, 1399, 1400, 1401, …….,1499, 1500, 1501,……., 1599, 1600,
1601, ….., 1699, 1700, 1701, ……, 1799, 1800, 1801,………, 1899, 1900,
1901, ……., 1999, 2000, 2001, ……., 2999, 3000, 3001, …….., 3999, 4000,
4001, ……, 4999, 5000, ……., 5999, 6000, ……, 6999, 7000, 7001, ………,
7999, 8000, 8001, ………., 8999, 9000, 9001, ……..,9999.
5-digit numbers:
10000, 10001, ……………………………………………………………, 19999,
20000, 20001, ………………………………………………………….., 29999,
30000, 30001, ………………………………………………………….., 39999,
40000, 40001, ………………, 49999, 50000, ………………………….., 59999,
60000, 60001, ……………, 69999, 70000, ……………………… ….., 79999,
80000, 80001, ……………., 89999, 90000, …………………………….. 99999
Now 6-digit numbers start with 99999 + 1 = 100000, i.e., hundred thousand.
1. Fill in
the blanks:
(i) 1,00,000
greater than 4,52,532 is …………….
(ii) 10,000,000
greater than 54,928,329 is …………….
(iii)
10,00,000 lower than 32,24,521 is …………….
(iv) 100,000
lower than 8,482,934 is …………….
(v) 10,000
greater than 99,999 is …………….
(vi) 1,000
greater than 56,784 is …………….
(vii) 10,000 much less
than 39,948 is …………….
Associated Idea
● Numbers Exhibiting on Spike Abacus.
● 1 Digit Quantity on Spike Abacus.
● 2 Digits Quantity on Spike Abacus.
● 3 Digits Quantity on Spike Abacus.
● 4 Digits Quantity on Spike Abacus.
● 5 Digits Quantity on Spike Abacus.
● Issues Associated to Place Worth.
● Expanded type of a Quantity.
● Instance on Comparability of Numbers.
● Successor and Predecessor of a Entire Quantity.
● Formation of Numbers with the Given Digits.
● Formation of Biggest and Smallest Numbers.
● Examples on the Formation of Biggest and the Smallest Quantity.
From Formation of Numbers to HOME PAGE
Did not discover what you had been in search of? Or wish to know extra data
about Math Solely Math.
Use this Google Search to seek out what you want.
[ad_2]