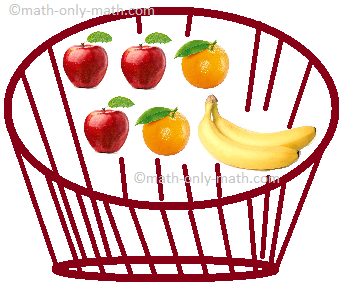[ad_1]
How one can discover fraction as part of assortment?
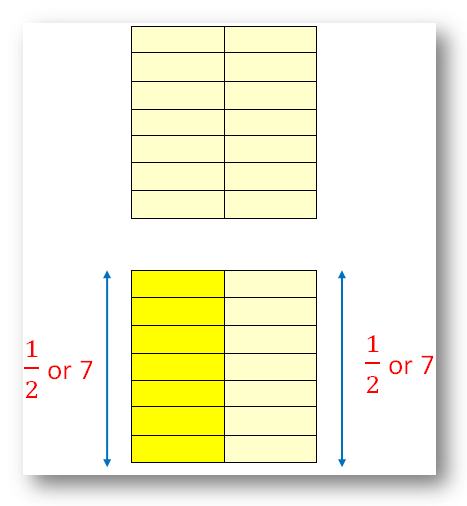
Let there be 14 rectangles forming
a field or rectangle.
Thus, it may be mentioned that there’s a assortment of 14 rectangles, 2 rectangles in every row.
Whether it is folded into two halves,
every half may have 7 rectangles. So, we will say one-half of 14 is 7.
Equally, one- half of 8 is 4 and
one-half of 16 is 8.
One-half of 8 squares = 4
Thus, 1/2 = 4/8
That’s, out of two equal components,
one half is 1.
Out of two equal components of 8 one
half is 4
|
One-half of a set of 8 cups Thus, 1/2 = 4/8 1 and 4 are numerators 2 and eight are denominators |
The denominator or backside quantity
of a fraction is the variety of equal components of a complete or a set. The numerator
or high variety of a fraction means what number of equal components of a complete or a
assortment is taken into account.
3/5, 7/8, 2/3, 5/12, 7/16, 11/25,
6/15 are all fractions.
The highest numbers of those fractions
are 3, 7, 2, 5, 7, 11 and 6. These numbers are referred to as high numbers or numerators
of the associated fractions.
The underside numbers of those
fractions are 5, 8, 3, 12, 16, 25 and 15. These numbers are referred to as backside
numbers or denominators of the associated fractions.
If we have now 2 bananas in a basket counting 7 fruits. What number of fruits have we in our complete set? What number of bananas have we in our complete set?
We have now 2 bananas out of seven fruits which could be written as (frac{2}{7}).
Within the determine under, the strip has been divided in 8 equal components. 3 components of the strip are shaded. The shaded half represents three-eight of the strip. We write this as (frac{3}{8}).
Variety of unshaded components are 5. Due to this fact, the unshaded half represents five-eight of this strip. We write this as (frac{5}{8}).
Within the fraction (frac{3}{8}), 3 represents the shaded a part of the gathering and the 8 represents the whole variety of components. 3 is numerator and eight is denominator of this fraction (frac{3}{8}).
A fraction is made up of two parts-numerator and denominator. The numerator is written above the denominator separated by a brief line.
Fractions additionally refer a part of the entire assortment or group.
|
Take a look at the picture- It’s a assortment of three flowers. What number of are blue? 2 out of the three flowers are blue. (frac{2}{3}) (frac{textrm{Blue Flowers (A part of Assortment)}}{textrm{Complete Flowers (The Entire Assortment)}}) (frac{2}{3}) of the flowers are blue. |
|
There are 4 vehicles in all. 3 vehicles are blue, 1 automotive is crimson. So, we will say – (frac{1}{4}) automotive is crimson and (frac{3}{4}) vehicles are blue |
The determine given under is a set of 6 circles. Draw a dotted line to divide the gathering into two equal components. Then, every half represents 3 circles. Additionally, every half incorporates 1/2
Therefore 1/2 of 6 =3.
The determine given under is a set of 8 circles.
Draw dotted traces to divide the gathering into 4 equal components.
Now, every half represents 1/4. Additionally, every half incorporates 2 circles.
Therefore, 1/4 of 8 = 2.
The determine alongside incorporates 12 circles.
Draw dotted traces to divide the gathering into 3 equal components.
Then every half represents 1/3.
Additionally, every half incorporates 4 circles.
Therefore, 1/3 of 12 =4.
2 components of the gathering characterize 2/3.
Additionally, 2 components comprise 8 circles.
Therefore, 2/3 of 12 = 8.
Associated Ideas
● Fraction as a A part of a Entire
● Convert a Fraction to an Equal Fraction
● Correct Fraction and Improper Fraction
From Fraction as a A part of Assortment to HOME PAGE
Did not discover what you have been in search of? Or need to know extra info
about Math Solely Math.
Use this Google Search to search out what you want.
[ad_2]