In Chapter 37 of “The Feynman Lectures on Physics Quantity 1,” Richard Feynman famously wrote that the thriller of wave-particle duality within the double-slit experiment is:

a phenomenon which is unattainable, completely unattainable to elucidate in any classical manner, and which has in it the center of quantum mechanics. In actuality, it incorporates the solely thriller. We can not make the thriller go away by “explaining” the way it works. We are going to simply inform you the way it works. In telling you the way it works we may have informed you concerning the fundamental peculiarities of all quantum mechanics.

On this Perception, I need to present you ways Brukner and Zeilinger’s information-theoretic precept of Info Invariance & Continuity as justified by the relativity precept solves this thriller. In How Quantum Info Theorists Revealed the Relativity Precept on the Basis of Quantum Mechanics, I defined how Info Invariance & Continuity entails that everybody measures the identical worth for Planck’s fixed h, whatever the relative spatial orientation of their inertial reference frames. Clearly, that may be justified by the relativity precept, i.e., the legal guidelines of physics (together with their constants of Nature) are the identical in all inertial reference frames, which I name “no most popular reference body (NPRF).” Whereas it’s generally assumed that totally different inertial reference frames are solely associated by totally different relative velocities, they’re in reality additionally associated by totally different relative spatial orientations, spatial places, and temporal places. The complete set of transformations between such reference frames that ensures everybody will measure the identical worth for the pace of sunshine c (the sunshine postulate of particular relativity), is the set of Poincare transformations, i.e., Lorentz boosts, spatial rotations, spatial translations, and time translations. The sunshine postulate is justified by the relativity precept and particular relativity (SR) follows from that truth, so I’ll characterize SR as following from NPRF + c. Likewise, the axiomatic reconstructions of QM based mostly on information-theoretic rules present how one can derive the (finite-dimensional) Hilbert area of QM from Info Invariance & Continuity, which will be justified by NPRF, so I’ll characterize QM as following from NPRF + h.

The axiomatic reconstructions of QM based mostly on information-theoretic rules render QM a precept principle, as I defined in A Precept Clarification of the “Mysteries” of Trendy Physics. Typically, a precept clarification fixing some thriller will be written:

Compelling elementary precept ##rightarrow## Justifies empirically found truth ##rightarrow## Dictating the thriller

On this case, we’ve got:

Relativity precept ##rightarrow## Justifies Info Invariance & Continuity ##rightarrow## Dictating wave-particle duality for the double-slit experiment

Recall from “How Quantum Info Theorists Revealed …” for the spin-##frac{1}{2}## particle, Info Invariance & Continuity entails that everybody measures the identical worth for h whatever the orientation of their Stern-Gerlach (SG) magnets, i.e., whatever the spatial orientation of their inertial reference frames. Since we’re speaking a couple of fixed of Nature having the identical worth in all inertial reference frames (associated on this case by spatial rotations), this empirically found truth will be justified by NPRF. To see how the classical formalism follows on common from the quantum formalism, I confirmed how the classical constructive account predicts that atomic dipoles alongside ##hat{z}## needs to be deflected by ##cos{left(theta proper)}## after they cross via SG magnets oriented at ##hat{b}## making an angle ##theta## with ##hat{z}##. As an alternative, we discover solely full deflections of ##pm 1## ##left(pm frac{hbar}{2}proper)## alongside ##hat{b}## that common to ##cos{left(theta proper)}##. This provides you ‘average-only’ projection of spin angular momentum between these reference frames as a consequence of NPRF + h.

For polarization, Info Invariance & Continuity entails that everybody measures the identical worth for h whatever the orientation of their polarizing filter, i.e., whatever the spatial orientation of their inertial reference frames, which is definitely justified by NPRF similar to the spin-##frac{1}{2}## particle. The empirically found truth on this case is {that a} photon both passes or it doesn’t cross via a polarizing filter, i.e., there aren’t any ‘partial photons’ handed by a polarizer. We will say that our empirically found truth on this case outcomes as a result of ##E = hf## and if a fractional photon handed via a polarizer, the worth of h could be lowered by that fraction, so you’ll have two inertial reference frames associated by a spatial rotation whereby h had two totally different values in violation of NPRF. This provides you ‘average-only’ transmission of polarized electromagnetic power between these reference frames as a consequence of NPRF + h. On this case, the classical wave mechanics follows on common from the distribution of photon (particle) power per quantum mechanics. Now let’s present an identical NPRF + h resolution to the thriller of wave-particle duality within the double-slit experiment.

Our measurement context will probably be an interference sample the place we are able to receive a wavelength ##lambda## whence momentum ##p = frac{h}{lambda}##. Meaning our qubit is that of Determine 1 with outcomes ##|textual content{BS Sure}rangle## of complete constructive interference at a most (Each Slits Sure) and ##|textual content{BS No}rangle## of complete harmful interference at a minimal (Each Slits No). [Since these are momentum states they are complementary to the “which slit” states ##|text{S1 Yes}rangle## (Slit 1 Yes) and ##|text{S2 Yes}rangle## (Slit 2 Yes) for position when measurements of position, momentum or superpositions thereof are being measured (Figure 2).] Our state is ##|psirangle = |textual content{BS Sure}rangle## and the measurement on this context will probably be a spatially localized detector moved a distance x alongside the interference sample from the central most towards a minimal on both facet (as proven in Figures 3 and 4). The quantity of momentum it data at every location alongside the interference sample depends upon how a lot constructive interference exists at that location, so it is going to begin from a most and regularly diminish to zero on the adjoining minimal the place there is no such thing as a constructive interference for the state ##|psirangle##.

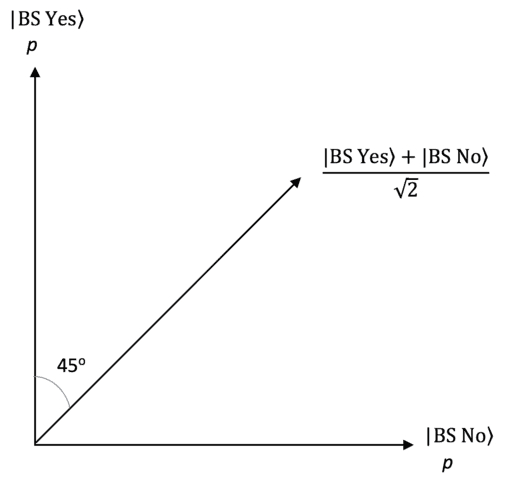
Determine 1. Hilbert Area Qubit for Momentum Measurements within the Double-slit Experiment.

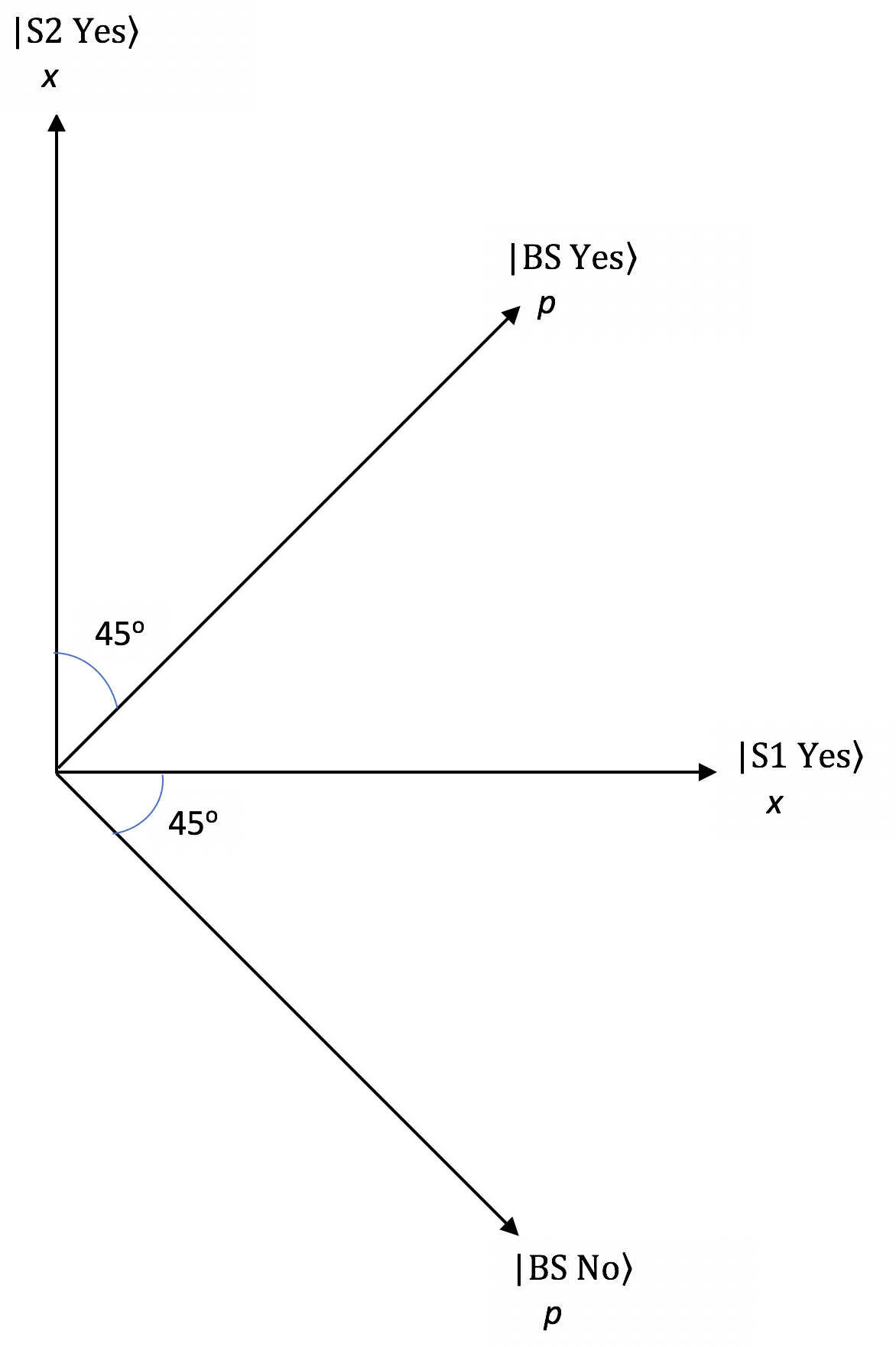
Determine 2. Hilbert Area Qubit for Measurements of Place, Momentum and Superpositions Thereof within the Double-slit Experiment.

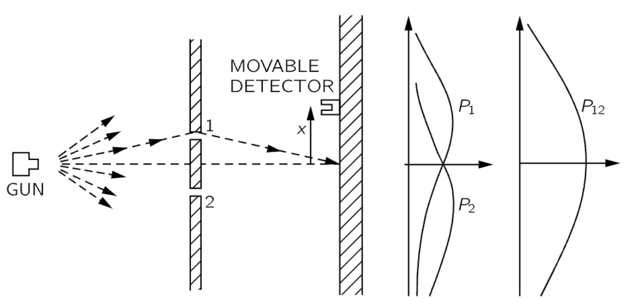
Determine 3. End result of the Double-slit Experiment with Bullets per Feynman.

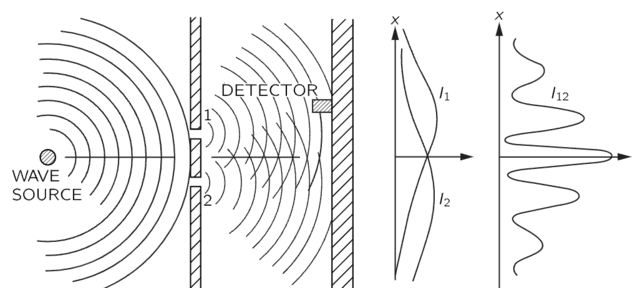
Determine 4. End result of the Double-slit Experiment with Water Waves per Feynman.

For instance, with ##|psirangle = |textual content{BS Sure}rangle## the electrical fields ##E_1 = E_2## of the electromagnetic waves from the 2 slits add in part on the central most to ##E_o## (say) and we’ve got complete constructive interference whereas they’re completely out of part and add to zero on the adjoining minimal. At any level between the central most and adjoining minimal the electrical subject amplitude is given by ##E_ocos{phi}## the place ##phi = frac{pi d sin{theta}}{lambda}## with the angle ##theta## and slit separation d as proven in Determine 5. So, when ##phi = frac{pi}{4}## the electrical subject is ##frac{E_o}{sqrt{2}}## and the electromagnetic wave depth (proportional to the wave momentum per the Poynting vector) is half that on the most. This can correspond to the Hilbert area vector ##frac{|textual content{BS Sure}rangle + |textual content{BS No}rangle}{sqrt{2}}## within the quantum case (Determine 1).

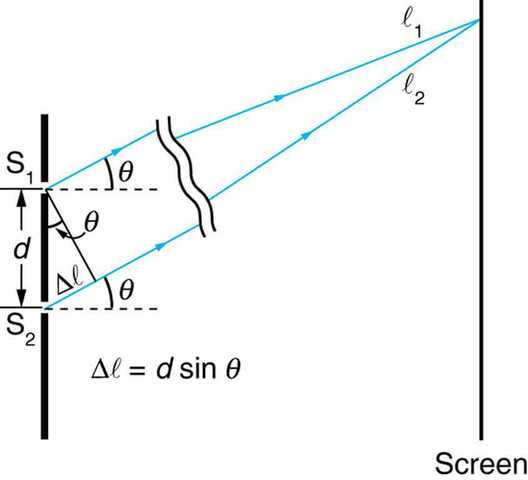
Determine 5. Double-slit Interference per Classical Wave Mechanics.

Mechanically talking, that is precisely how Zeilinger’s experiment labored in Determine 6 the place his detector recorded counts over a 60-second time interval at every location alongside the interference sample (see additionally Feynman’s variations of the double-slit experiment with bullets, water waves and electrons in Chapter 37 of “The Feynman Lectures on Physics Quantity 1,”). A classical wave measurement of this kind would receive momentum in a continuum sense (like water waves in Determine 4), somewhat than discrete detector clicks (like bullets in Determine 3), at every spatial location. After all, every detector click on represents a quantum of momentum/power, so counting detector clicks continues to be a measurement of momentum (over the realm of the detector the place every click on delineates a unit of time).

Determine 6. Double-slit Experiment Outcomes per Zeilinger [1].

As with the polarization experiment, we then cut back the speed at which momentum is emitted by the supply in order that just one quantum of momentum ##p = frac{h}{lambda}## is ‘passing via’ the slits at a time. The classically steady wave description says p will probably be distributed spatially alongside the detector, so our spatially localized momentum measurement described above will measure a fraction of the momentum ##p = frac{h}{lambda}## at any given location x, which implies h is lowered exactly by that very same fraction within the inertial reference body at x. Since fractional measurements of h are forbidden by NPRF (our inertial reference frames listed below are associated by spatial translations in x), our momentum measurements at every level x as a substitute receive a lot of quanta (every with the identical worth for h in ##p = frac{h}{lambda}##) per fastened time (60 seconds in Zeilinger’s experiment). These counts are then normalized relative to that on the central most for our quantum distribution, in order that the continuum distribution of momentum alongside the interference sample predicted by the classical wave interference evaluation obtains on common.

This clarification of the double-slit experiment per NPRF + h and the qubit reveals that Feynman was primarily appropriate. The thriller of the double-slit experiment resides in the truth that NPRF + h calls for we receive quanta of momentum ##p = frac{h}{lambda}## within the inertial reference frames related to the places x (as with bullets in Determine 3), somewhat than a continuum of wave depth (as with water waves in Determine 4). Nevertheless, the quantum measurement context is that for momentum p, so an interference sample permitting us to compute ##lambda## to be used in ##p = frac{h}{lambda}## is required. Subsequently, the interference sample per classical wave mechanics is what should receive on common on this quantum mechanics context as within the momentum measurement of Zeilinger’s Determine 6. That’s, the thriller of wave-particle duality within the double-slit experiment follows from the truth that the quantum case doesn’t conform to the classical case of particles or the classical case of waves, however have to be a mix of each as a result of NPRF + h. In all three examples, NPRF + h calls for {that a} classically steady amount (angular momentum, polarization, momentum) be quantized, in order that you must take a mean to get well the classical continuity. That’s how quantum info principle’s precept of Info Invariance & Continuity, as justified by the relativity precept, solves what Feynman referred to as “the solely thriller” of QM in precept vogue.

1. Anton Zeilinger, “Why the quantum? ‘It’ from ‘bit’? A participatory universe? Three far-reaching challenges from John Archibald Wheeler and their relation to experiment,” in Science and Final Actuality: Quantum Idea, Cosmology and Complexity, John D. Barrow, Paul C.W. Davies and Charles L. Harper, Jr. (eds.), (Cambridge Univ Press, Cambridge, 2004), pp 201-220.