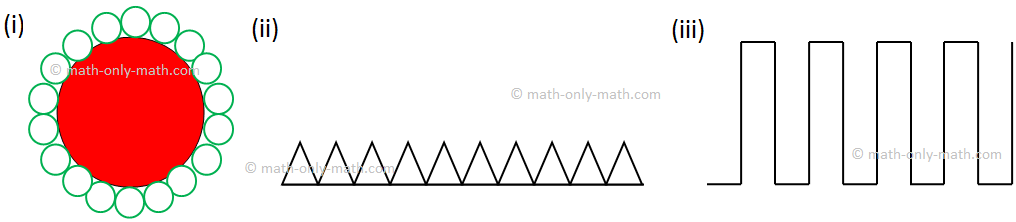Idea of sample will assist us to be taught the essential quantity patterns and desk patterns.

Animals corresponding to all cows, all lions, all canines and all different animals have dissimilar options. All mangoes have comparable options and shapes. Leaves of the identical tree have comparable sample of form. The doorways and home windows of a home have comparable patterns. We could seek for comparable patterns in arithmetic additionally.

The examine of patterns helps college students to look at relationships and discover steady connections, to infer generalizations and predictions.

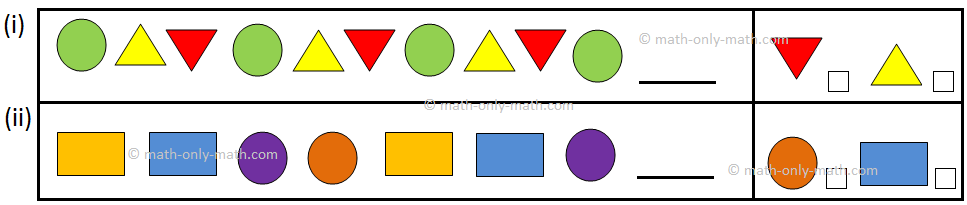
1. Observe the sample and tick the one that ought to come subsequent.

2. Full the patterns by coloring the shapes.

3. Observe the sample of numbers and write those that ought to come subsequent.

1. Observe the sample and tick the form that ought to come subsequent.

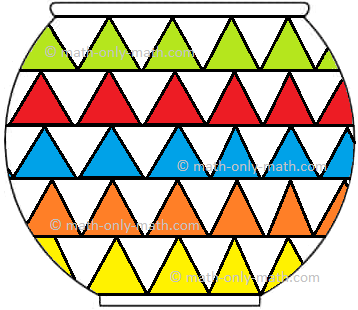
Similar shapes may be colored otherwise to create patterns.

This row of squares has been colored following the color code RYGB.

R for Pink

Y for Yellow

G for Inexperienced and

B for Blue

Extra rows may be added following the same code. Color the grid following the color code given beneath.

RYGB

YGBR

GBRY

BRYG

You’ll have seen such patterns in patchwork quilts.

Color sample in patch work quilt

Observe these patterns in your environment.

Sample of straight strains and curved strains on a fence

Chessboard sample

Sample of bricks on a wall

In on a regular basis life we observe costume sample, carpet sample, wall-paper sample, sari-design sample in addition to quantity sample in arithmetic.

Examples of patterns are given beneath:

2     4      6     8     10     12    …………….;                    

5    10    15    20    25    30    …………….

The learner has to acknowledge a sample and broaden it. He should analyze it after which create new patterns to check the subject material. The instructor ought to develop within the college students the idea of sample.

(i) To get higher thought on the idea of sample allow us to have a look at the next photos:

Utilizing the numbers the
sequence is:

The rule to go from one quantity to the subsequent quantity is ‘add 2’

(ii) Within the sample 1, 3, 5, 7, ……. the variety of footballs go on
growing and the quantity turns into bigger every time.

Typically the numbers i8n a sample go on reducing.
Suppose there are 16 footballs within the basket. An individual offers two footballs to
every group of gamers for the soccer match. The variety of footballs within the
basket goes on reducing by every group.

The sample is:

The lacking numbers are 8, 6 and 4. The rule of the sample
is to remove 2 every time.

(iii) The numbers turns into bigger and bigger very quickly.

The lacking quantity is 16. The rule to go from one time period to the subsequent is multiply by 2.

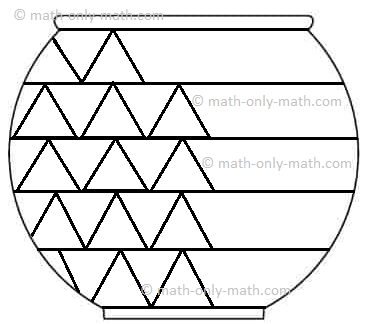
Listed here are some examples of designs having the identical sample:

Quantity Patterns:

1 + 2 + 3 + 4 + 5 + ……. + 10 = 55

Sum of the numbers from 1 to 10 is 55

Therefore, the sum of the numbers from 11 to twenty will likely be 10 × 10 = 100 greater than 55

11 + 12 + 12 + ……. + 20 = 155

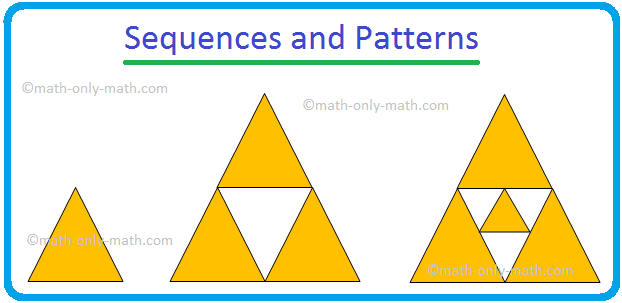
Have a look at the next sample that grows while you add triangles.

The sample
may be represented in numbers as 1, 2, 3.

A sample
like given above will kind a sequence 1, 4, 9, 16, 25, …..

Desk Patterns:

(i) 2, 4, 6, 8, 10, …….

In desk 2, we see each ahead quantity is 2 greater than its
earlier one.

(ii) 2, 8, 14, 20, 26, …….

Each ahead quantity is 6 greater than the earlier one.

Questions and Solutions on Idea of Sample:

I. Observe the rule and write the subsequent quantity within the
sequence.

(i) 5, 10, 15, 20, …….., …….., …….., …….., ……..,
……..

(ii) 1, 2, 3, …….., …….., …….., …….., ……..,
…….., ……..

(iii) 10, 20, …….., …….., …….., …….., ……..,
…….., …….., ……..

(iv) 10, 9, 8, …….., …….., …….., …….., ……..,
…….., ……..

Reply:

I. (i) 25, 30, 35, 40, 45, 50

(ii) 4, 5, 6, 7, 8, 9, 10

(iii) 30, 40, 50, 60, 70, 80, 90, 100

(iv) 7, 6, 5, 4, 3, 2, 1

A quantity sequence follows a sample. We are able to make quantity
patterns by making use of a rule.

II. Make a quantity sequence by making use of the given rule.

Reply:

II. (i) 4, 6, 8, 10

(ii) 90, 80, 70, 60

(iii) 8, 12, 16, 20

(iv) 6, 9, 12, 15

III. Full the given sample. One is finished for you.

Reply:

III.

IV. Draw a zebra crossing sample within the following area.

Reply:

IV.

V. Proceed the sample.

Reply:

V.

VI. Full the sample and shade.

Reply:

VI.

VII. Discover the rule used on this quantity sample.

(i) 55, 45, 35, 25, … _______________

(ii) 36, 39, 42, … _______________

(iii) 50, 45, 40, 35, … _______________

(iv) 10, 20, 30, 40, … _______________

Reply:

VII. 

(i) -10

(ii) +3

(iii) -5

(iv) +10

VIII. Tick the form that comes subsequent.

Reply:

VIII.

IX. Have a look at the image and write the solutions.

(i) What form is used on this sample?

(ii) What number of occasions is the form used?

(iii) What number of white sq. bins are there?

(iv) What number of black sq. bins are there?

(v) Do you see any quantity sample?

Reply:

IX.

(i) Sq.

(ii) 64

(iii) 32

(iv) 32

X. Full and shade the sample.

Reply:

X.

IX. Draw the subsequent sample within the given image.

Reply:

IX.

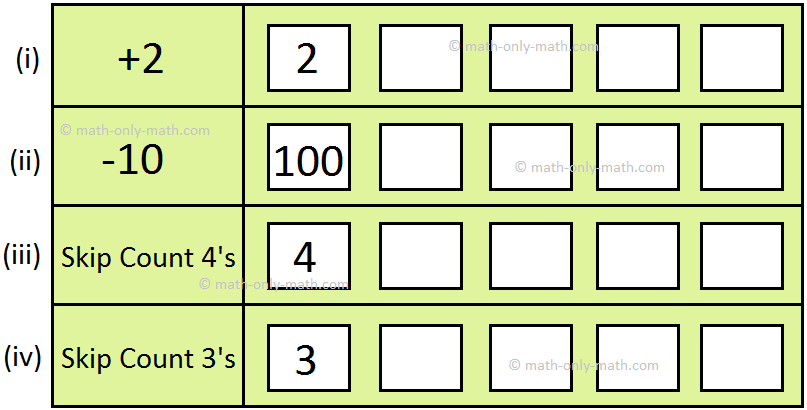
X. Observe the rule and write what comes subsequent.

(i) 110, 120, 130, _____, _____, _____, _____, _____.

(ii) 2, 4, 6, _____, _____, _____, _____, _____.

(iii) 90, 89, 88, _____, _____, _____, _____, _____.

(iv) 16, 20, 24, _____, _____, _____, _____, _____.

Reply:

X. (i) 140, 150, 160, 170, 180.

(ii) 8, 10, 12, 14, 16.

(iii) 87, 86, 85, 84, 83.

(iv) 28, 32, 36, 40, 44.

2nd Grade Math Apply

From Idea of Sample to HOME PAGE