
[ad_1]
Summary
Richard Pierce describes the intention of his e-book [2] about associative algebras as his try to show that there’s algebra after Galois concept. Whereas Galois concept would possibly probably not be on the agenda of physicists, many algebras are: from tensor algebras as the robe for infinitesimal coordinates over Graßmann and Banach algebras for the idea of differential types and capabilities as much as Lie and Virasoro algebras in quantum physics and supermanifolds. This text is supposed to supply a information and a presentation of the principle elements of this zoo of algebras. And we’ll meet many well-known mathematicians and physicists on the best way.
Definitions and Distinctions
Algebras
An algebra ##mathcal{A}## is within the first place a vector house. This supplies already two vital distinguishing options: the dimension of ##mathcal{A}##, i.e. whether or not it’s an ##n##- or infinite-dimensional vector house, and the attribute of the sphere, i.e. the quantity ##p## such that
$$
underbrace{1+1+ldots+1}_{textual content{p-times}}=0
$$
The attribute of a area is at all times a first-rate ##p##, e.g. ##2## in case of a lightweight change, or a Boolean algebra, or set to ##0## if the sphere comprises the rational numbers. Observe that ##0## is the cardinality of the empty set. We wouldn’t have a separate identify if an algebra was solely a vector house. The defining property for an algebra is its multiplication; neither the multiplication with scalars that stretches and compresses vectors that it already has as a vector house, nor the interior product of actual vector areas that produces angles. It’s a second binary operation on its vectors that has once more a vector consequently and the one necessities are the distributive legal guidelines
$$
(vec{x}+vec{y})cdot vec{z}=vec{x}cdot vec{z}+vec{y}cdotvec{z}textual content{ and }vec{z}cdot (vec{x}+vec{y})=vec{z}cdotvec{x}+vec{z}cdot vec{y}.
$$
The cross product in ##mathbb{R}^3## is such an instance. Nevertheless, the multiplication in ##mathcal{A}=left(mathbb{R}^3,timesright)## is neither commutative nor associative. An algebra is a hoop that additionally occurs to be a vector house, which a hoop, on the whole, is just not. This illustrates the broad selection algebras have: finite-dimensional or not, attribute constructive or not, commutative or not, associative or not, and all properties rings can have, like being Artinian or Noetherian, or just whether or not there’s a ##1.## Pierce has ##37## specs in his index beneath the key phrase algebra, and his e-book is barely about associative algebras!
Subspaces, Subalgebras, Beliefs
If ##mathcal{A}## is an algebra, then the vector subspaces of it are of little curiosity in the event that they haven’t any connection to the multiplication. We subsequently primarily think about subalgebras ##mathcal{S},## i.e. vector subspaces of ##mathcal{A}## which fulfill the situation
$$
mathcal{S}cdot mathcal{S} subseteq mathcal{S}.
$$
However even subalgebras have a giant drawback. If we think about the quotient (or generally issue) house
$$
mathcal{A}/mathcal{S}=left{a+mathcal{S},|,ain mathcal{A}proper}={ain mathcal{A}}+mathcal{S}
$$
then we wish to outline a multiplication
$$
(a+mathcal{S})cdot (b+mathcal{S})=acdot b +mathcal{S}quad (*)
$$
For ##a,bin mathcal{A}## and ##s,tin mathcal{S}## we get
start{align*}
(a+s)cdot (b+t) &=acdot b + (acdot t) +(scdot b)+scdot t finish{align*}
The primary time period ##acdot b## is what we goal at, and the final time period ##scdot tin mathcal{S}## makes no drawback, however we have now no management over the 2 phrases within the center. They even rely on the representatives ##s,t## we select from ##mathcal{S}.## Because of this our try at a definition of multiplication is just not well-defined. ##mathcal{A}/mathcal{S}## remains to be a vector house, however not an algebra. To beat these obstacles we require that
$$
mathcal{A}cdot mathcal{S} subseteq mathcal{S} textual content{ and }mathcal{S}cdot mathcal{A} subseteq mathcal{S}quad (**)
$$
Because of this the phrases within the center are elements of ##mathcal{S}##
and ##(*)## is well-defined:
$$
mathcal{A}/mathcal{S}ni (a+s)cdot (b+t) =acdot b + underbrace{(acdot t) +(scdot b)+scdot t}_{in S} in mathcal{A}/mathcal{S}
$$
Subalgebras ##mathcal{S}subseteq mathcal{A}## which have the extra property ##(**)## are referred to as beliefs of ##mathcal{A}.## Two-sided beliefs to be precise. These with ##mathcal{A}cdot mathcal{S} subseteq mathcal{S}## are referred to as left beliefs, and people with ##mathcal{S}cdot mathcal{A} subseteq mathcal{S}## are referred to as proper beliefs. In fact, the excellence is out of date in commutative algebras. If ##mathcal{S}subseteq mathcal{A}## is a perfect then
$$
{0} rightarrow mathcal{S} stackrel{iota}{rightarrowtail } mathcal{A} stackrel{pi}{twoheadrightarrow} mathcal{A}/mathcal{S}rightarrow {0}
$$
is a brief precise sequence of algebra homomorphisms, i.e. the picture of 1 mapping is the kernel of the following mapping, and the mappings obey
$$
varphi (acdot b)=varphi (a)cdot varphi (b)
$$
The phrases Artinian and Noetherian which are inherited by the ring construction of an algebra should be distinguished by left and proper and they aren’t symmetric. Proper-Artinian (right-Noetherian) implies that the descending (ascending) chain situation holds for the lattice of proper beliefs shaped by inclusion, i.e. each chain of proper beliefs comprises a minimal (maximal) proper superb. The definition of Left-Artinian (left-Noetherian) algebras are accordingly. That is solely fascinating for infinite-dimensional algebras since beliefs are at all times vector subspaces. Algebras ##mathcal{A}## with out correct beliefs, i.e. beliefs aside from ##{0}## and ##mathcal{A},## are referred to as easy, and semisimple if they’re a direct sum of those. Necessary two-sided beliefs of an algebra are its middle
$$
mathcal{Z(A)}={zin mathcal{A},|,zcdot a= acdot ztext{ for all }ain mathcal{A}}
$$
and its radical, the intersection of all beliefs ##mathcal{S}## such that ##mathcal{A}/mathcal{S}## is straightforward. They play a vital position within the concept of non-semisimple algebras, e.g. nilpotent algebras, i.e. algebras ##mathcal{A}## such that ##mathcal{A}^n={0}## for some ##n in mathbb{N}.##
Nearly Fields
Fields are trivially one-dimensional algebras over themselves. The complicated numbers are a two-dimensional actual algebra. There are additionally algebras which are very near fields: the Hamiltonian quaternions ##mathbb{H}## which aren’t commutative however in any other case obey all area axioms as e.g. the existence of a multiplicative impartial ingredient ##1## and inverse components. These algebras are referred to as division algebras. If we drop the requirement of an associative multiplication, too, then we receive the division algebra of the octonions ##mathbb{O}## that are an eight-dimensional actual algebra. These two are crucial examples. They’re the one ones over the actual numbers apart from ##mathbb{C},## and finite, associative division algebras are already fields.
The Large Common Ones
I don’t wish to drift into class concept the place the mathematical time period common is exactly outlined so this title needs to be taken with a pinch of salt. It might probably imply mathematically common just like the tensor algebra, or virtually common just like the matrix algebras as illustration areas. Anti-commutativity and gradation are the opposite two instruments to acquire vital algebras.
Matrix Algebras
Matrix teams function linear representations in group concept
start{align*}
varphi , : ,G&longrightarrow operatorname{GL}(n,mathbb{F})
varphi (acdot b)&=varphi (a)cdot varphi (b)
finish{align*}
and the identical do matrix algebras for associative algebras
start{align*}
varphi , : ,mathcal{A}&longrightarrow mathbb{M}(n,mathbb{F})
varphi (acdot b)&=varphi (a)cdot varphi (b)
finish{align*}
and for Lie algebras
start{align*}
varphi , : ,mathfrak{g}&longrightarrow mathfrak{gl}(n,mathbb{F})
varphi ([a,b])=[varphi (a),varphi (b)]&=varphi (a)cdot varphi (b)-varphi (b)cdot varphi (a)
finish{align*}
The concept behind (finite-dimensional) linear representations of algebras is to check the conduct of matrices on the suitable facet of the equation which we have now a mighty device for with the idea of linear algebra with a purpose to study one thing concerning the algebra multiplication on the left facet of the equation. The complete classification of semisimple Lie algebras is predicated on this precept.
Tensor Algebras
A tensor algebra ##mathcal{A}=T(V)## over a vector house ##V## is as common as you will get. We take vectors ##v,win V## and outline
$$
vcdot w = votimes w
$$
as an associative, distributive – means bilinear – multiplication. Because the consequence needs to be in ##T(V)## once more, we receive arbitrary, however finitely lengthy chains ##v_1otimes v_2otimes ldotsotimes v_n in T(V)## in order that
$$
T(V)=bigoplus_{n=0}^infty V^{otimes_n}
$$
the place ##V^{otimes_0}=mathbb{F}## is the scalar area, ##V^{otimes_1}=V,## ##V^{otimes_2}=operatorname{lin ,span},v,win V## and so forth. The multiplication ##votimes w## might be considered the rank one matrix we get once we multiply a column vector with a row vector: ##n## copies of the row weighted by the entries of the column. ##uotimes votimes w## will then change into a rank one dice and so on. The tensor algebra doesn’t carry any properties of some multiplication since we solely used the vector house for its development and the tensors might be seen as purely formal merchandise. This property makes the tensor algebra additionally technically a common algebra. Moreover, it permits the technical modifications of indices that physicists carry out on tensors.
Graßmann Algebras
The wedge product, higher, the multiplication within the Graßmann algebra ##mathcal{A}=G(V)## over a vector house ##V## is much like that of a tensor algebra. The one distinction is, that the wedge product is moreover anti-commutative, i.e.
$$
vwedge w + wwedge v=0
$$
which is equal to $$vwedge v=0$$ if the attribute of the sphere is just not ##2.## It’s formally the quotient algebra
$$
G(V)=T(V)/langle votimes w + wotimes v rangle = bigoplus_{n=0}^infty V^{wedge_n}
$$
alongside the best generated by the tensors ##votimes w + wotimes v ## to supply anti-commutativity. It’s mainly a tensor algebra that is aware of what orientation is. One can consider a wedge product ##v_1wedge ldots wedge v_nin V^{wedge_n}## as an ##n##-dimensional quantity of a parallelepiped. Volumes are oriented, and 0 if they’re really an space, i.e. if two spanning vectors are equal and the thing has a dimension much less. Graßmann algebras are important in homological algebra, e.g. to outline the Cartan-Eilenberg complicated of Lie algebras, and differential geometry the place they’re used to outline the outside (Cartan) derivatives on differential types.
Graded Algebras
A graded algebra is a direct sum of vector subspaces over a set of discrete parameters whose multiplication is related to the gradation. Tensor and Graßmann algebras are examples of algebras graded over non-negative integers. In these circumstances we have now multiplications
$$
V^{otimes_n}otimes V^{otimes_m}subseteq V^{otimes_{n+m}}; , ;V^{wedge_n}wedge V^{wedge_m}subseteq V^{wedge_{n+m}}
$$
Multivariate polynomials construct a graded algebra, too. They type a vector house and might be multiplied. The gradation is alongside their general diploma
$$
mathcal{A}=bigoplus_{d=0}^infty mathbb{F}^{(d)}[X_1,ldots ,X_m] textual content{ with }mathbb{F}^{(d)}=langle X_{1}^{r_{1}}cdots X_{m}^{r_{m}}mid r_{1}+ldots +r_{m}=drangle .
$$
and are topic to algebraic geometry.
Not all gradations are by non-negative integers. Lie superalgebras
$$
mathcal{L} =mathcal{L}_0 oplus mathcal{L}_1
$$ are graded by ##mathbb{Z}_2## and the gradation is extra immediately associated to the multiplication. The prefix tremendous is used at any time when the gradation is ##mathbb{Z}_2.## Let’s be aware the grade of a component by ##|v|in mathbb{Z}_2={0,1}## for ##vin mathcal{L}.## The diploma of a product is then
$$
|[v,w]|=|v|+|w| pmod{2}
$$
and the defining equations of the Lie superalgebra are
start{align*}
textual content{tremendous skew-symmetry}, :& ;
[v,w]&+(-1)^[w,v]=0
textual content{tremendous Jacobi identification}, :& ;
(-1)^[u,[v,w]]&+(-1)^v[v,[w,u]]+(-1)^[w,[u,v]]=0
finish{align*}
The even half ##mathcal{L}_0## is an odd Lie algebra.
Evaluation
We assume that the underlying area of all algebras thought of on this part is at all times the actual numbers ##mathbb{R}## or the complicated numbers ##mathbb{C}.## In fact, there are such unique areas like a p-adic evaluation however these constructions gained’t be the topic of analytical algebras on this article.
Features
We didn’t think about capabilities to date, besides polynomials. However capabilities are essential in all STEM areas and they are often multiplied. Furthermore, they usually have further properties like continuity or smoothness which construct giant lessons of vital capabilities. Additionally they have norms like as an example the uniform norm (supremum) for bounded capabilities. Concerns like this result in the idea of Banach algebras.
A Banach algebra ##mathcal{B}##, named after the Polish mathematician Stefan Banach (1892-1945), is an associative actual or complicated algebra over a whole, normed vector house which is sub-multiplicative
$$
|,fcdot g,|leq |f|cdot|g| textual content{ for all }f,gin mathcal{B}
$$
The quaternions are an actual, nevertheless, not complicated (Banach) algebra. Its middle is the actual numbers, so the complicated numbers can’t be the scalar area of the quaternions. If we drop the requirement of completeness then we communicate of a normed algebra. A Banach##{^{boldsymbol *}}##-algebra, generally referred to as a ##mathbf{C^*}##-algebra or involutive Banach algebra, is a posh Banach algebra ##mathcal{B}## with an involution ##{}^*##. An involution is a mapping
start{align*}
{}^*; &: ;mathcal{B}longrightarrow mathcal{B}&cr
textual content{involutive}; &: ;left(left(fright)^*proper)^*=f&textual content{ for all }fin mathcal{B}cr
textual content{anti-commutative}; &: ;(fcdot g)^*=g^*cdot f^*&textual content{ for all }f,gin mathcal{B}cr
textual content{conjugate linear}; &: ;(alpha f+beta g)^*=bar alpha f^*+bar beta g^*&textual content{ for all }f,gin mathcal{B}, ; ,alpha,betain mathbb{C}cr
mathrm{C}^*textual content{ property}; &: ;|f^*cdot f|=|f|^2&textual content{ for all }fin mathcal{B}
finish{align*}
There are such a lot of examples that it might require a separate therapy to even listing the vital ones. One is the house of steady complicated capabilities ##mathcal{B}=mathrm C(Okay)## on a compact house ##Okay## with pointwise addition and multiplication, the uniform norm
$$
|f|=displaystyle{sup_{xin Okay}}|f(x)|
$$
and the involution
$$
f^*(x)=overline{f(x)},,
$$
one other the continual, linear operators on a posh Hilbert house. There are even subclasses of ##C^*##-algebras that carry their very own names. E.g., a ##mathbf{H^*}##-algebra ##mathcal{B}## is a ##mathrm{C^*}##-algebra such that its norm is outlined by an interior product (which explains the H for Hilbert house) and for all ##a,f,gin mathcal{B}##
$$
langle af,grangle =langle f,a^{*}grangle , wedge ,
langle fa,grangle =langle f,ga^{*}rangle.
$$
A ##mathbf{W^*}##-algebra or von-Neumann-algebra ##mathcal{B}=L(H)## is an unital ##mathrm{C^*}##-subalgebra of bounded linear operators ## L(H)## on a Hilbert house ##H## which is closed underneath the weak operator topology (subsequently the letter W). It has been referred to as the ring of operators in older texts, and is now named after the Hungarian mathematician Neumann János Lajos (1903-1957) higher often known as Johann or John von Neumann.
Measures
Measure concept is one other option to strategy evaluation, particularly the combination a part of it. The commonest measure is the Lebesgue measure which generalizes the Riemann integration we discovered in school. I at all times preferred to consider it as an integration that ignores detachable singularities and different negligible inconveniences. In fact, such a viewpoint is comfy however not fairly proper. A greater rationalization might be present in [6]. The formal strategy to generalize the measures that we use for integration is by ##sigma ##-algebras.
A ##boldsymbol sigma ##-algebra ##mathcal{A}=mathcal{R}(X)## is a nonvoid household of subsets of a given set ##X## such that
start{align*}
Ain mathcal{R}(X); &Longrightarrow ;Xbackslash Ain mathcal{R}(X)
A,Bin mathcal{R}(X); &Longrightarrow ;Acup Bin mathcal{R}(X)
A,Bin mathcal{R}(X); &Longrightarrow ;Acap (Xbackslash B)in mathcal{R}(X)
displaystyle{{A_n,|,nin mathbb{N}}subseteq mathcal{R}(X)}; &Longrightarrow ;displaystyle{bigcup_{n=1}^infty A_nin mathcal{R}(X)}
finish{align*}
This purely set-theoretical assemble turns into our integration measure with further restrictions. It’s for my part additionally the one affordable begin to chance concept. If ##X## is a domestically compact Hausdorff house and ##mathcal{O}## the household of open units of ##X.## Then we denote the intersection of all ##sigma ##-algebras of subsets ##mathcal{O}subseteq Y subseteq X## by ##mathcal{I(O)}.## Thus ##mathcal{I(O)}## is the smallest ##sigma ##-algebra of subsets of ##X## containing all open units of ##X## and is named Borel-##boldsymbolsigma ##-algebra ##mathcal{B}(X)=mathcal{I(O)}## of ##X.## It makes ##X## a measure house and the units in ##mathcal{B}(X)## measurable. This was most likely the shortest introduction to Borel-##sigma ##-algebras ever and but, it illustrates that the world of study is a really totally different one if we strategy it by way of measure concept. An vital Borel measure on domestically compact topological teams ##G##, e.g. on sure Lie teams, is the Haar measure ##mu##. It has some further, technical properties, specifically regularity, and most vital, left invariance
$$
int_G f(g.x),dmu = int_G f(x),dmu
$$
which makes it the measure of alternative in Lie concept.
Lie Algebras
Lie algebras are roughly talking the tangent areas to Lie teams, that are topological teams such that inversion and multiplication are analytical capabilities, at their identification ingredient. Their multiplication ##[cdot,cdot]## is anti-commutative like that of Graßmann algebras of differential types
$$
[x,y]+[y,x]=0,
$$
and obeys the Leibniz rule of differentiation, which we name Jacobi identification in Lie algebras.
$$
[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0
$$
If Lie algebras are themselves matrix algebras, or are represented by these, then their multiplication is the commutator of matrices
$$
[x,y]=xcdot y-y cdot x
$$
The precise definition by way of tangent areas, i.e. vector fields requires a bit extra care and technical precision. For his or her algebraic construction, nevertheless, we solely want the equations above. I don’t know any class of algebras that makes use of extra names of scientists to explain sure sorts of subalgebras, in addition to sure Lie algebras. Lie algebras themselves are named after the Norwegian mathematician Marius Sophus Lie (1842-1899).
Subalgebras
A Lie subalgebra such that the left-multiplication by its components
$$
operatorname{advert}x, : ,y longmapsto [x,y],
$$
the adjoint illustration, are all nilpotent, is named an Engel subalgebra, named after the German mathematician Friedrich Engel (1861-1941). A minimal Engel subalgebra is named a Cartan subalgebra, normally abbreviated by CSA, named after the French mathematician Élie Joseph Cartan (1869-1951). A maximal solvable subalgebra is named a Borel subalgebra, named after the French mathematician Félix Édouard Justin Émile Borel (1871-1956), and a maximal toral subalgebra is named Maltsev subalgebra named after the Russian mathematician Anatoly Ivanovich Maltsev (1909-1967).
Each Lie algebra might be written as a semidirect sum of a semisimple subalgebra (direct sum of easy subalgebras) and its maximal solvable superb, its radical. The straightforward (no correct beliefs) Lie algebras are all categorised. There are 4 infinite collection of easy matrix algebras (these with hint zero, even-dimensional orthogonal, odd-dimensional orthogonal, symplectic) and 5 so-called distinctive easy Lie algebras. The solvability of the unconventional ##mathfrak{R}## implies that the collection
$$
[ldots [[[mathfrak{R},mathfrak{R}],[mathfrak{R},mathfrak{R}]],[[mathfrak{R},mathfrak{R}],[mathfrak{R},mathfrak{R}]]]ldots]
$$
will find yourself within the trivial superb ##{0}.## Solvable Lie algebras are removed from any form of classification.
Examples
Whereas the names of Lie subalgebras learn because the who-is-who of mathematicians who handled Lie concept, the listing of examples learn as a who-is-who of well-known physicists.
There’s the three-dimensional, nilpotent Heisenberg algebra, which is the Lie algebra of strict higher ##3times 3## matrices, and its generalizations named after the German physicist Werner Karl Heisenberg (1901-1976); the six-dimensional tangential house of the invariance group ##O(3,1)## of Minkowski house, the Lorentz algebra, named after the Dutch physicist Hendrik Antoon Lorentz (1853-1928); the ten-dimensional tangential house of an invariance group in electrodynamics, and later in particular relativity concept, the Poincaré algebra, named after the French mathematician and physicist Jules Henri Poincaré (1854-1912); the Witt algebra, an infinite-dimensional, graded Lie algebra of complicated vector fields named after the German mathematician Ernst Witt (1911-1991); the infinite-dimensional Virasoro algebra, a central extension of a Witt algebra, named after the Argentinian physicist Miguel Ángel Virasoro (1940-2021).
Particular Constructions
Now we have already seen the definition of Lie superalgebras as ##mathbb{Z}_2## graded Lie algebras the place the gradation immediately impacts the multiplication guidelines. One other development is an associative algebra, the common enveloping algebra ##boldsymbol U(mathfrak{g})## of a Lie algebra ##mathfrak{g}.## The identify is a powerful trace. Now we have once more a quotient algebra of the associative tensor algebra ##T(mathfrak{g})## over the vector house ##mathfrak{g}.## The best we issue out shall replicate the Lie multiplication
$$
U(mathfrak{g}) = T(mathfrak{g})/langle xotimes y – yotimes x -[x,y] rangle ,
$$
therefore we establish the weather ##[x,y]## with ##xotimes y-yotimes x.##
Kac-Moody algebras, named after the Russian mathematician Victor Gershevich (Grigorievich) Kac (1943-) and the Canadian mathematician Robert Vaughan Moody (1941-), generalize the idea of semisimple Lie algebras based mostly on their development from generalized Cartan matrices.
Extra Nice Scientists
Jordan Algebras
Jordan algebras are to some extent a counterpart of Lie algebras. They’re named after the German physicist Ernst Pascual Jordan (1902-1980). If we have now an arbitrary associative algebra ##mathcal{A},## then
$$
xcirc y = [x,y] = xy-yx
$$
defines a Lie algebra, and
$$
xcirc y = dfrac{xy+yx}{2}
$$
defines a Jordan algebra. The precise definition, nevertheless, is in fact with out an underlying associative algebra. A Jordan algebra is outlined as a commutative algebra for which the Jordan identification holds
$$
(xy)(xx)=x(y(xx)).
$$
It follows from a non-trivial argument that even
$$
(x^m y) x^n=x^m(yx^n) , textual content{ for },m,nin mathbb{N}
$$
holds. Jordan algebras ##mathcal{J}## that consequence from an underlying associative algebra are referred to as particular Jordan algebras, the others distinctive Jordan algebras. There is just one complicated, distinctive Jordan algebra
$$
E_3=M(3,8)=left{left.mathbb{C}cdotbegin{pmatrix}a&x&ybar x&b&z bar y&bar z&cend{pmatrix};proper|; a,b,cin mathbb{R}, , ,x,y,zin mathbb{O}proper}
$$
##E_3## is phenomenal as a result of the quaternions ##x,y,z## should not associative.
There are a lot of extra sorts of Jordan algebras like Jordan superalgebras, Jordan Banach algebras, quadratic Jordan algebras, or infinite-dimensional Jordan algebras. In ##1979,## the Russian-American mathematician Efim Isaakovich Zelmanov (1955-) categorised infinite-dimensional easy (and prime non-degenerate) Jordan algebras. They’re both of Hermitian or Clifford kind. Particularly, the one exceptionally easy Jordan algebras are ##27##-dimensional Albert algebras. They’re named after the American mathematician Abraham Adrian Albert (1905-1972).
Clifford Algebras
Clifford algebras ##mathcal{C}## are algebras which are a bit tough originally. We want a scalar area ##mathbb{F},## finite-dimensional vector house ##V##, an extra vector that serves as ##1_Cin mathcal{C}## and a quadratic type ##Q## on ##V.## Then ##mathcal{C}=mathit{Cl}(V,Q)## is the biggest associative, not essentially commutative algebra over ##mathbb{F}## that’s generated by ##V## and ##1_C## such that
$$
vcdot v=-Q(v) cdot 1_C
$$
They’re named after the British thinker and mathematician William Kingdon Clifford (1845-1879). Clifford algebras play an vital position in differential geometry and quantum physics. This turns into clearer if we have a look at Graßmann algebras once more. If we think about the Graßmann algebra ##G(V)## over an actual, finite-dimensional vector house ##V## and the trivial quadratic type ##Q=0## then
$$
G(V) = mathit{Cl}(V,0).
$$
If we begin with a Clifford algebra, then we get a Graßmann algebra by
$$
vwedge w :=dfrac{1}{2}(vcdot w-wcdot v).
$$
Furthermore, we will understand any Clifford algebra inside a Graßmann algebra by setting
$$
v cdot w := vwedge w -Q(v,w).
$$
The best Clifford algebra is the actual, two-dimensional algebra that we get if we select ##V=mathbb{R}cdot mathrm{i}## and ##Q(v)=v^2.## From this we get for ##v=rmathrm{i},w=smathrm{i}##
start{align*}
(v+alpha 1_C)(w+beta 1_C)&= (rmathrm{i}+alpha)(smathrm{i}+beta)= dfrac{s}{r}cdot(rmathrm{i}+alpha)left(rmathrm{i}+dfrac{r beta}{s}proper)
&=dfrac{s}{r}left( Q(v,v)+ left(dfrac{r^2beta}{s}+alpha rright)mathrm{i} +dfrac{ralpha beta}{s} proper)
&=dfrac{s}{r}left(-r^2++dfrac{ralpha beta}{s}proper)+(rbeta+alpha s)mathrm{i}
&=(alpha beta – rs)+(rbeta+alpha s)mathrm{i}
finish{align*}
that are simply the complicated numbers thought of as actual vector house. We will get the quaternions in an analogous means if we think about the actual, associative hull of ##V=mathbb{R}mathrm{i}oplus mathbb{R}mathrm{j}## and ##1_C.## The true vector house is two-dimensional, the actual Clifford algebra four-dimensional since ##mathrm{i}cdot mathrm{j}=mathrm{okay}##.
Hopf Algebras
Hopf algebras ##mathcal{H}## are named after the German-Swiss mathematician Heinz (Heinrich) Hopf (1894-1971). They’re bi-algebras which are concurrently unital associative algebras and counital coassociative coalgebras. What which means illustrates the next commutative diagram
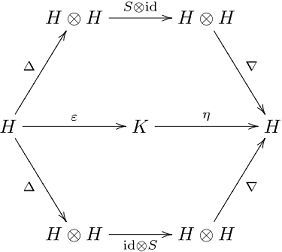
The linear mapping ##S, : ,mathcal{H}longrightarrow mathcal{H}## is named the antipode of
$$
mathcal{H}=(mathcal{H}, , ,nabla, , ,eta, , ,Delta, , ,epsilon, , ,S)
$$
the place
$$
S astoperatorname{id}=eta circ epsilon = operatorname{id}ast S
$$
with a product referred to as folding in order that the antipode is the inverse ingredient of the identification mapping. It isn’t shocking that particulars change into shortly relatively technical. I discussed them as a result of they’ve various functions in physics and string concept. A easy instance for a Hopf algebra is a gaggle algebra ##mathcal{H}=mathbb{F}G## the place ##G## is a gaggle and
$$
Delta(g)=gotimes g; , ;epsilon(g)=1; , ;S(g)=g^{-1}.
$$
One other pure instance is the common enveloping algebra ##U(mathfrak{g})## of a Lie algebra ##mathfrak{g}## which turns into a Hopf algebra ##mathcal{H}=(U(mathfrak{g}),nabla,eta,Delta,epsilon,S)## by
$$
Delta(u)=1otimes u +uotimes 1; , ;epsilon(g)=0; , ;S(u)=-u.
$$
This makes Hopf algebras related for the cohomology concept of Lie teams. There are extra instance listed on Wikipedia [8].
Boolean Algebras
Boolean algebras are named after the British mathematician and logician George Boole (1815-1864). They’re algebras over the sphere ##mathbb{F}_2={0,1}.## They’ve the binary and unary logical operations
$$
textual content{AND, OR, NEGATION}
$$
or likewise the binary and unary set operations
$$
textual content{UNION, INTERSECTION, COMPLEMENT}.
$$
Boolean algebras are vital for combinational circuits and theoretical pc science. E.g. the well-known NP-complete satisfiability drawback SAT is an announcement about expressions in a Boolean algebra. Their formal definition includes a couple of dozen of guidelines that we don’t must quote right here.
Epilogue
There are a lot of extra algebras with particular properties, e.g., a not essentially associative baric algebra ##mathcal{A}_b## that has a one-dimensional linear illustration, i.e. a homomorphism into the underlying area of scalars. If this mapping is surjective then it’s referred to as weight operate, which explains the identify.
A commutative algebra ##mathcal{G}## with a foundation ##{v_1,ldots,v_n}## is named a genetic algebra if
start{align*}
v_i cdot v_j &=sum_{okay=1}^n lambda_{ijk} v_k
lambda_{111}&=1
lambda_{1jk}&=0text{ if }okay<j
lambda_{ijk}&=0text{ if }i,j >1 textual content{ and }okay leq max{i,j}
finish{align*}
holds. Each genetic algebra is at all times a baric algebra [5]. An instance of eye colours as a genetic trait might be discovered within the answer manuals [7] (March 2019, web page 422 within the full file).
I hope I’ve piqued your curiosity on the planet of algebras. It’s a enormous world with many nonetheless anonymous objects. Who is aware of, perhaps certainly one of them will bear your identify sooner or later.
Sources
Sources
[1] Edwin Hewitt, Karl Stromberg, Actual and Summary Evaluation, Springer Verlag, Heidelberg, 1965, GTM 25
https://www.amazon.com/Summary-Evaluation-Graduate-Texts-Arithmetic/dp/0387901388/
[2] Richard S. Pierce, Associative Algebras, Springer Verlag, New York, 1982, GTM 88
https://www.amazon.com/Associative-Algebras-Graduate-Texts-Arithmetic/dp/0387906932/
[3] James E. Humphreys, Introduction to Lie Algebras and Illustration Principle, Springer Verlag, New York, 1972, GTM 9
https://www.amazon.com/Introduction-Algebras-Illustration-Graduate-Arithmetic/dp/3540900535/
[4] Joachim Weidmann, Lineare Operatoren in Hilbert Räumen, Teubner Verlag, Stuttgart, 1976
[5] Rudolph Lidl, Günter Pilz, Angewandte abstrakte Algebra II, Bibliographisches Institut, Zürich, 1982
https://www.amazon.com/Angewandte-abstrakte-Algebra-II/dp/3411016213/
[6] Member micromass, Omissions in Arithmetic Schooling: Gauge Integration
https://www.physicsforums.com/insights/omissions-mathematics-education-gauge-integration/
[7] Answer Manuals
https://www.physicsforums.com/threads/solution-manuals-for-the-math-challenges.977057/
[8] Wikipedia
https://en.wikipedia.org/wiki/Main_Page
https://de.wikipedia.org/wiki/Wikipedia:Hauptseite
[9] nLab
https://ncatlab.org/nlab/present/HomePage
[10] Image
[ad_2]