
[ad_1]
We’ll introduce the elemental counting precept with an instance. This counting precept is all about decisions we would make given many potentialities.
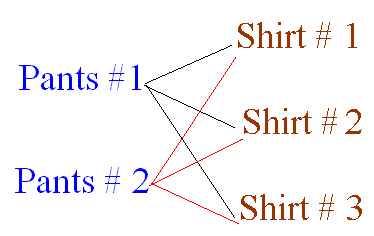
Multiplication precept
Suppose most of your garments are soiled and you’re left with 2 pants and three shirts.
What number of decisions do you’ve gotten or what number of other ways are you able to gown?
Let’s name the pants: pants #1 and pants #2
Let’s name the shirts: shirt #1, shirt #2, and shirt #3
Then, a tree diagram because the one above can be utilized to point out all the alternatives you may make.
As you may see on the diagram, you may put on pants #1 with shirt # 1. That is one in all your decisions.
Rely all of the branches to see what number of decisions you’ve gotten.
Since you’ve gotten six branches, you’ve gotten 6 decisions.
Nonetheless, discover {that a} fast multiplication of two × 3 will yield the identical reply.
Typically, suppose you’ve gotten n decisions or n methods for a primary activity and m decisions or m methods for a second activity.
In line with the multiplication precept, additionally known as multiplication rule, you’ve gotten n × m decisions or n × m methods for each duties.
Within the instance above, you’ve gotten 2 decisions for pants and three decisions for shirts. Thus, you’ve gotten 2 × 3 decisions.
A pair extra examples exhibiting how one can use the multiplication precept
Instance #1:
You go a restaurant to get some breakfast. The menu says pancakes, waffles, or house fries. And for drink, espresso, juice, scorching chocolate, and tea. What number of totally different decisions of foods and drinks do you’ve gotten?
There 3 decisions for meals and 4 decisions for drink.
Thus, you’ve gotten a complete of three × 4 = 12 decisions.
Instance #2:
You throw a die twice.
The primary time you throw the die, the variety of decisions is n = 6.
The second time you throw the die, the variety of decisions is m = 6.
Thus, you’ve gotten a complete of m × n = 6 × 6 = 36 decisions.
Addition precept
Within the instance above, you needed to put on each a shirt and pants. In different conditions, the selection is yours to do one or the opposite.
For instance, suppose you go to a restaurant and there are 10 pork dishes and 15 lamb dishes. If you’ll both eat a pork dish or a lamb dish however not each, then you need to use the addition precept.
What number of other ways are you able to eat?
In the event you select a pork dish, then you’ve gotten 10 totally different decisions
In the event you select a lamb dish, then you’ve gotten 15 totally different decisions
The full variety of methods you may eat is 10 + 15 = 25
Typically, suppose you’re coping with disjoint occasions or occasions that can’t happen on the similar time.
If have x decisions or x methods for a primary activity and y decisions or y methods for a second activity.
In line with the addition precept, additionally known as rule of sum, you’ve gotten x + y decisions or x + y methods for each duties.
Utilizing each the multiplication precept and the addition precept
For instance, suppose you go to a restaurant and there are 3 hen dishes and a couple of beef dishes. Your objective is to select both a hen dish or a beef dish. Then, for dessert, you’ll select amongst 3 totally different flavors of ice-cream (vanilla, chocolate, and strawberry).
What number of other ways you may eat?
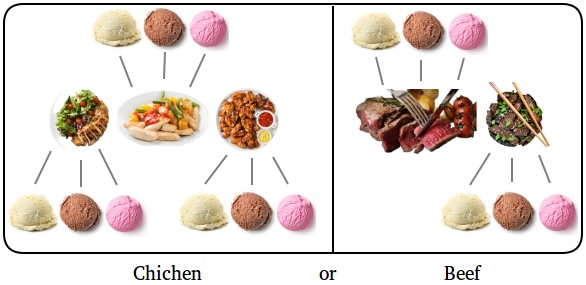
In the event you select a hen dish, then you’ve gotten 3 decisions for hen and three decisions for the ice-cream.
The variety of decisions for hen and ice-cream is 3 × 3 = 9
In the event you select a beef dish, then you’ve gotten 2 decisions for beef and three decisions for the ice-cream.
The variety of decisions for beef and ice-cream is 2 × 3 = 6
The full variety of decisions is 3 × 3 + 2 × 3 = 9 + 6 = 15
A pleasant basic counting precept quiz is given under so that you can confirm if this lesson is clearly understood.
[ad_2]