
[ad_1]
A conditional likelihood accommodates a situation which forces you to focus your consideration to a subset of the pattern area. For instance, an organization might have men and women working for the corporate. Nevertheless, chances are you’ll need to reply questions on males solely or females solely. In case you are coping with insurance coverage, chances are you’ll need to reply questions on people who smoke solely or non-smokers solely.
A great way to get began with conditional possibilities is to make use of a contingency desk.
Conditional likelihood utilizing a contingency desk
Right here is tips on how to discover the conditional likelihood utilizing a contingency desk that we used within the lesson about marginal likelihood. The desk exhibits check outcomes for 200 college students who took a GED check.
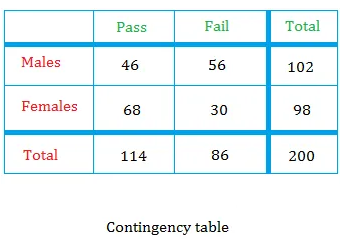
From the record of 200 college students, we choose a scholar randomly. Nevertheless, suppose that you simply already know the coed chosen is a male.
The truth that the coed is a male implies that the occasion has already occurred. And it forces you to focus your consideration solely on males or 102 potential outcomes.
What’s conditional likelihood?
Understanding that the scholar is a male, you’ll be able to calculate the likelihood that this scholar has handed or failed. This sort of likelihood is known as conditional likelihood
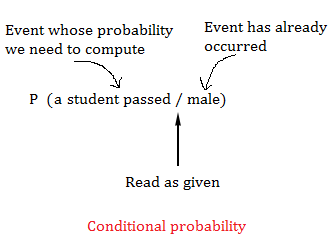
The notation to search out the likelihood that ‘a scholar has handed if the coed is male is
P(a scholar has handed / male)
You might the truth is compute any of the next 8 conditional possibilities:
- P(a scholar has handed / male)
- P(a scholar has handed / feminine)
- P(a scholar has failed / male)
- P(a scholar has failed / feminine)
- P(a scholar is male / handed)
- P(a scholar is male / failed)
- P(a scholar is feminine / handed)
- P(a scholar is feminine / failed)
A few examples displaying tips on how to discover the conditional likelihood utilizing a contingency desk
Instance #1
Allow us to compute the P(a scholar has handed / male).
If the coed is male, then the coed might be picked from the record of 102 males.
From this record solely 46 college students have handed.

Variety of males who handed
Whole variety of males
46
102
= 0.451
Instance #2
What about P(a scholar is male / handed) ?
The variety of college students who handed is the same as 114.
From this record, solely 46 college students are males.
a scholar is a male
Variety of college students who handed
46
104
= 0.403
As you’ll be able to see from the outcomes P(a scholar has handed / male) is just not equal to
P(a scholar is male / handed) as a result of there’s a distinction.
P(a scholar has handed / male): This likelihood simply exhibits the success charge of males solely.
P(a scholar is male / handed): This likelihood compares the success charge of males to females.
Conditional likelihood components
Take an in depth look once more on the following ratio:
Variety of males who handed
Whole variety of males
Let M be the occasion ‘the coed is a male’
Let P be the occasion ‘the coed has handed’
Let P∩M be the occasion ‘the coed is a male and has handed’
n(P∩M) = variety of male college students who handed = 46
n(M) = complete variety of male college students = 102
n(P ∩ M)
n(M)
46
102
= 0.451
We are able to get the identical reply utilizing likelihood as a substitute of counting. Divide the numerator and the denominator of the ratio instantly above by 200.
46 / 200
102 / 200
0.23
0.51
= 0.451
P(P∩M) = likelihood {that a} scholar has handed if the coed is male = 46 / 200 = 0.23
P(M) = likelihood {that a} scholar is male = 102 / 200 = 0.51
P(P ∩ M)
P(M)
We are able to then conclude that there are two methods to discover a conditional likelihood.
The best way to discover the conditional likelihood by counting
In case you are coping with equally probably outcomes similar to tossing a coin or a good die with six sides, then for any two occasions A and B, you should utilize the next components:
n(A ∩ B)
n(B)
The best way to discover the conditional likelihood by utilizing the definition of conditional likelihood
Whether or not you might be coping with equally probably outcomes or not, then for any two occasions A and B, you should utilize the next components:
P(A ∩ B)
P(B)
The likelihood of A given B is the ratio of the likelihood of the intersection of A and B to the likelihood of B.
Extra examples of conditional likelihood
Instance #3
A card is drawn at random from a regular deck. The cardboard is just not changed. Discover the likelihood that the second card is a king on condition that the primary card drawn was a king.
Let K1 be occasion ‘the primary card drawn is a king’ and K2 be the occasion ‘the second card drawn is a king’
If a king is drawn and never changed, then there are 3 kings left and the deck will now have 51 playing cards.
P(K2 / K1) = 3/51 ≈ 0.0588
Two occasions A and B are known as impartial occasions if P(A / B) = P(A)
Instance #4
Let H1 be the occasion that the primary toss of a coin is a head and let H2 be the occasion that the second toss of the coin is a head. Present that H1 and H2 are impartial occasions.
Your calculations should present that P(H2 / H1) = P(H2)
The total pattern area is {HH, HT, TH, TT}
H2 = {HH, TH} and P(H2) = 0.50
On condition that the primary toss is a head, we find yourself with {HH, HT} and we’re restricted to those two outcomes to compute P(H2 / H1)
From these two outcomes, we see that HH (half of the two outcomes) has a head because the second toss.
P(H2 / H1) = 0.5
P(H2 / H1) = P(H2) = 0.5, and thus H1 and H2 are impartial occasions.
In impartial occasions, the prevalence of an occasion doesn’t affect the prevalence of one other occasion. In instance #4, the occasion ‘you get a head with the primary toss or H1’ won’t affect the probability of getting once more a head with the second toss.
This isn’t the case with instance #3 the place the prevalence of an occasion can affect the prevalence of one other.
Two occasions A and B are known as dependent occasions if P(A / B) ≠ P(A)
In instance #3, P(K2 / K1) = 3/51. Nevertheless, P(K2) = 4/52 = 0.076
For the reason that first card was not changed or put again within the deck, the likelihood of the second draw clearly is determined by the result of the primary,
[ad_2]